Page 522 - Mathematical Techniques of Fractional Order Systems

Characteristics system.

Main 2 0:0138Þ 2 1:5008Þ 2 5Þ 2 8:480Þ 2 0:7Þ 2 0:3622Þ

& conservative 1) 0.4, (0.0522,0,-2.6585)
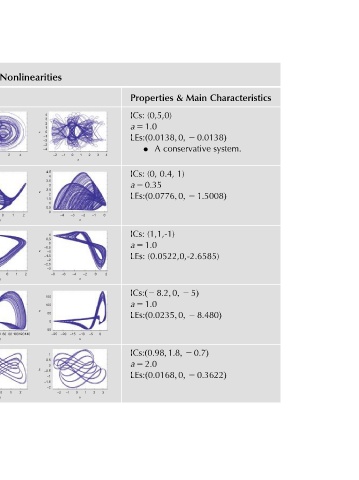
Properties (0,5,0) ICs: a 5 1:0 LEs:ð0:0138; 0; A (0, ICs: a 5 0:35 LEs:ð0:0776; 0; (1,1,-1) ICs: a 5 1:0 LEs: ICs:ð2 8:2; 0; a 5 1:0 LEs:ð0:0235; 0; ICs:ð0:98; 1:8; a 5 2:0 LEs:ð0:0168; 0;

4 2
0 3
0
3 0
–1 2
2 –5
–2 –2 1
1 x x –10 x x
x 0
0 –3 –4 –15 –1
–1 –2 4.5 4 3.5 3 2.5 2 1.5 1 0.5 0 –4 1 0.5 0 –0.5 –1 –1.5 –2 –2.5 –3 –6 –8 150 100 50 0 –50 –20 –25 1 0.5 0 –0.5 –1 –1.5 –2 –2
Nonlinearities 4 3 2 1 0 z –1 –2 –3 –4 4 z 2 z 2 1 z z 2
0 2 y 1 0 -1 y 0 –1 –2 y 20 40 60 80 100120140 y 1 0 –1 y
Quadratic 4 3 2 1 0 z –1 –2 –3 –4 –2 –4 4.5 4 3.5 3 2.5 z 2 1.5 1 0.5 0 -2 1 0.5 0 –0.5 z –1 –1.5 –2 –2.5 –3 –3 150 100 z 50 0 –50 –40–20 0 1 0.5 0 z –0.5 –1 –1.5 –2 –2 –3

and 4 3 2 0 –1 2 0 0 –5 3 2 1
Equilibria Attractor 1 0 –1 –2 x –2 –3 –4 x –2 –4 –6 x –10 –15 –20 –25 x 0 –1 –2 x

No 4 2 0 y –2 –4 2 1 0 y –1 –2 2 1 0 y –1 –2 –3 –8 140 120 100 80 60 y 40 20 0 –20 –40 2 1 0 y –1 –2 –3
With

Attractors

Hidden Equations y 52 x 2 zy z 5 y 2 2 a z 5 2y 2 1 xz 2 a z 52 y 1 0:1x 2 1 1:1xz 1 a x 52 0:1y 1 a z 5 xz 2 3y y 52 2x 2 z z 52 y 2 1 z 2 1 a

17.1 x 5 y _ _ _ _ x 52 y _ y 5 x 1 z _ _ x 5 y _ y 5 z _ _ _ y 5 x 1 z _ x 5 2y _ _ _
TABLE (1) (2) (3) (4) (5)