Page 779 - Mechanical Engineers' Handbook (Volume 2)

770 Control System Design Using State-Space Methods

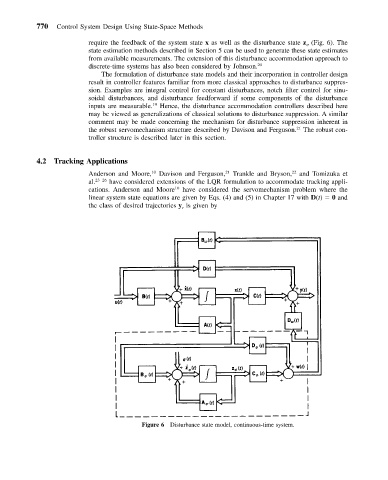
require the feedback of the system state x as well as the disturbance state z (Fig. 6). The

state estimation methods described in Section 5 can be used to generate these state estimates
from available measurements. The extension of this disturbance accommodation approach to
discrete-time systems has also been considered by Johnson. 20
The formulation of disturbance state models and their incorporation in controller design
result in controller features familiar from more classical approaches to disturbance suppres-
sion. Examples are integral control for constant disturbances, notch filter control for sinu-
soidal disturbances, and disturbance feedforward if some components of the disturbance
inputs are measurable. 19 Hence, the disturbance accommodation controllers described here
may be viewed as generalizations of classical solutions to disturbance suppression. A similar
comment may be made concerning the mechanism for disturbance suppression inherent in
21
the robust servomechanism structure described by Davison and Ferguson. The robust con-
troller structure is described later in this section.

4.2 Tracking Applications
Anderson and Moore, 10 Davison and Ferguson, 21 Trankle and Bryson, 22 and Tomizuka et
al. 23–26 have considered extensions of the LQR formulation to accommodate tracking appli-
cations. Anderson and Moore 10 have considered the servomechanism problem where the
linear system state equations are given by Eqs. (4) and (5) in Chapter 17 with D(t) 0 and
the class of desired trajectories y is given by
r

Figure 6 Disturbance state model, continuous-time system.