Page 787 - Mechanical Engineers' Handbook (Volume 2)

778 Control System Design Using State-Space Methods

lim e(t) 0 (77)
t→
for all e(t ). If the system under consideration is time invariant, the eigenvalues of the matrix
0
A LC govern the transient behavior of the estimation error. These eigenvalues, referred
to as observer poles, can be arbitrarily located in the complex plane by appropriate choice
of the constant observer gain matrix L if and only if the system given by Eqs. (4) and (5)
in Chapter 17 is completely reconstructible. 28 For LTI systems, reconstructibility is exactly
equivalent to observability. Also, if the L matrix is to be real, the complex eigenvalues of
A LC should be specified as conjugate pairs.
3
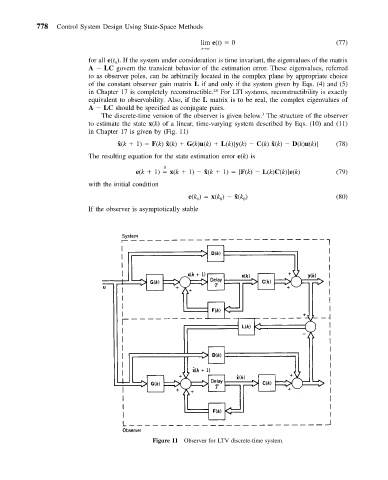
The discrete-time version of the observer is given below. The structure of the observer
to estimate the state x(k) of a linear, time-varying system described by Eqs. (10) and (11)
in Chapter 17 is given by (Fig. 11)
ˆ x(k 1) F(k) ˆx(k) G(k)u(k) L(k)[y(k) C(k) ˆx(k) D(k)u(k)] (78)

The resulting equation for the state estimation error e(k)is

e(k 1) x(k 1) ˆx(k 1) [F(k) L(k)C(k)]e(k) (79)
with the initial condition
e(k ) x(k ) ˆx(k ) (80)
0
0
0
If the observer is asymptotically stable

Figure 11 Observer for LTV discrete-time system.