Page 1016 - The Mechatronics Handbook

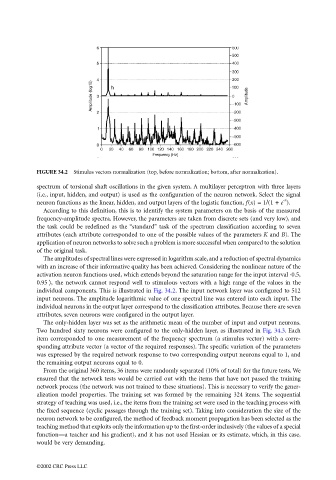
FIGURE 34.2 Stimulus vectors normalization (top, before normalization; bottom, after normalization).
spectrum of torsional shaft oscillations in the given system. A multilayer perceptron with three layers
(i.e., input, hidden, and output) is used as the configuration of the neuron network. Select the signal
-x
neuron functions as the linear, hidden, and output layers of the logistic function, f(x) = 1/(1 + e ).
According to this definition, this is to identify the system parameters on the basis of the measured
frequency-amplitude spectra. However, the parameters are taken from discrete sets (and very low), and
the task could be redefined as the “standard” task of the spectrum classification according to seven
attributes (each attribute corresponded to one of the possible values of the parameters K and B). The
application of neuron networks to solve such a problem is more successful when compared to the solution
of the original task.
The amplitudes of spectral lines were expressed in logarithm scale, and a reduction of spectral dynamics
with an increase of their informative quality has been achieved. Considering the nonlinear nature of the
activation neuron functions used, which extends beyond the saturation range for the input interval ·0.5,
0.95 〉, the network cannot respond well to stimulous vectors with a high range of the values in the
individual components. This is illustrated in Fig. 34.2. The input network layer was configured to 512
input neurons. The amplitude logarithmic value of one spectral line was entered into each input. The
individual neurons in the output layer correspond to the classification attributes. Because there are seven
attributes, seven neurons were configured in the output layer.
The only-hidden layer was set as the arithmetic mean of the number of input and output neurons.
Two hundred sixty neurons were configured to the only-hidden layer, as illustrated in Fig. 34.3. Each
item corresponded to one measurement of the frequency spectrum (a stimulus vector) with a corre-
sponding attribute vector (a vector of the required responses). The specific variation of the parameters
was expressed by the required network response to two corresponding output neurons equal to 1, and
the remaining output neurons equal to 0.
From the original 360 items, 36 items were randomly separated (10% of total) for the future tests. We
ensured that the network tests would be carried out with the items that have not passed the training
network process (the network was not trained to these situations). This is necessary to verify the gener-
alization model properties. The training set was formed by the remaining 324 items. The sequential
strategy of teaching was used, i.e., the items from the training set were used in the teaching process with
the fixed sequence (cyclic passages through the training set). Taking into consideration the size of the
neuron network to be configured, the method of feedback moment propagation has been selected as the
teaching method that exploits only the information up to the first-order inclusively (the values of a special
function—a teacher and his gradient), and it has not used Hessian or its estimate, which, in this case,
would be very demanding.

©2002 CRC Press LLC