Page 77 - A Course in Linear Algebra with Applications

3.1: The Definition of a Determinant 61

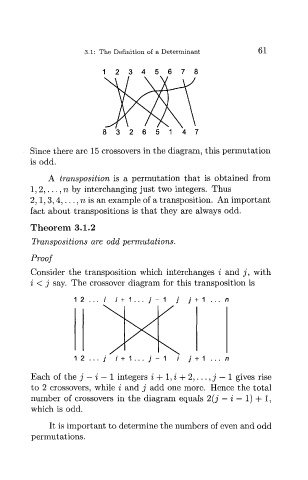
1 2 3 4 5 6 7 8

8 3 2 6 5 1 4 7

Since there are 15 crossovers in the diagram, this permutation
is odd.

A transposition is a permutation that is obtained from
2
1, ,..., n by interchanging just two integers. Thus
2,1, ,4,..., n is an example of a transposition. An important
3
fact about transpositions is that they are always odd.
Theorem 3.1.2

Transpositions are odd permutations.
Proof

Consider the transposition which interchanges i and j , with
i < j say. The crossover diagram for this transposition is

1 2 . . . / / + 1 . . . j - 1 j j + 1 . . . n

1 2 . . . j i + 1 . . . j - 1 / j + 1 . . . n

Each of the j — i — 1 integers i + 1, i + 2,..., j — 1 gives rise
to 2 crossovers, while i and j add one more. Hence the total
number of crossovers in the diagram equals 2(j — i — 1) + 1,
which is odd.

It is important to determine the numbers of even and odd
permutations.