Page 559 - Advanced_Engineering_Mathematics o'neil

15.3 Bessel Functions 539

1 0.5
x
1 2 3 4 5 6 7
0.8 0

0.6 –0.5
0.4 –1

0.2 –1.5
–2
0
0 2 4 6 8 10 12
x –2.5
–0.2
–3
–0.4

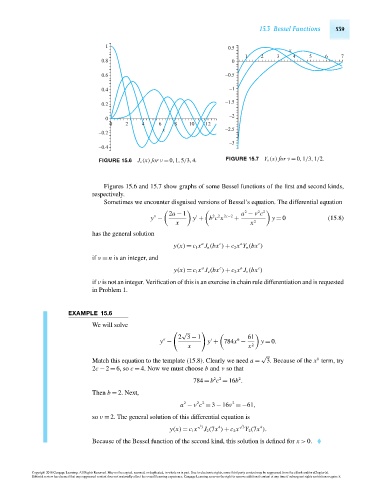
FIGURE 15.6 J ν (x) for ν = 0,1,5/3,4. FIGURE 15.7 Y ν (x) for ν = 0,1/3,1/2.

Figures 15.6 and 15.7 show graphs of some Bessel functions of the first and second kinds,
respectively.
Sometimes we encounter disguised versions of Bessel’s equation. The differential equation
2a − 1 a − ν c

2 2 2
2 2 2c−2
y − y + b c x + y = 0 (15.8)
x x 2
has the general solution
c
c
a
a
y(x) = c 1 x J n (bx ) + c 2 x Y n (bx )
if ν = n is an integer, and
a
c
a
c
y(x) = c 1 x J ν (bx ) + c 2 x J ν (bx )
if ν is not an integer. Verification of this is an exercise in chain rule differentiation and is requested
in Problem 1.
EXAMPLE 15.6
We will solve
√
2 3 − 1
61
6
y − y + 784x − y = 0.
x x 2
√
b
Match this equation to the template (15.8). Clearly we need a = 3. Because of the x term, try
2c − 2 = 6, so c = 4. Now we must choose b and ν so that
2
2 2
784 = b c = 16b .
Then b = 2. Next,
2
2 2
2
a − ν c = 3 − 16ν =−61,
so ν = 2. The general solution of this differential equation is
√ 3 4 √ 3 4
y(x) = c 1 x J 2 (7x ) + c 2 x Y 2 (7x ).
Because of the Bessel function of the second kind, this solution is defined for x > 0.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 15:20 THM/NEIL Page-539 27410_15_ch15_p505-562