Page 151 - Advanced Thermodynamics for Engineers, Second Edition
P. 151
138 CHAPTER 6 FINITE TIME (OR ENDOREVERSIBLE) THERMODYNAMICS
Derive all the necessary equations, but assume the Carnot efficiency, h ¼ 1 T C /T H .
[0.75; 0; 0.5; 100; 1000 K; 500 K]
P6.2 A heat engine operates between two finite reservoirs, initially at 800 and 200 K, respectively.
The temperature of the hot reservoir falls by 1 K for each 1 kJ extracted from it, while the
temperature of the cold reservoir rises by 1 K for each 1 kJ added. What is the maximum work
output from the engine as the reservoir temperatures equalise? Is the equalisation temperature
for maximum work a higher or lower limit of the equalisation temperature?
[200 kJ; lower]
P6.3 Closed cycle gas turbines operate on the internally reversible Joule cycle with an efficiency of
1
h Joule ¼ 1 ðk 1Þ=k
r p
where r p ¼ pressure ratio of the turbine and k ¼ ratio of specific heats, c p /c v ¼ 1.4.
This equation significantly overestimates the efficiency of the cycle when external
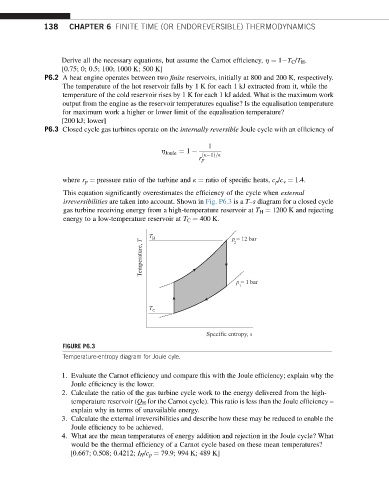
irreversibilities are taken into account. Shown in Fig. P6.3 is a T–s diagram for a closed cycle
gas turbine receiving energy from a high-temperature reservoir at T H ¼ 1200 K and rejecting
energy to a low-temperature reservoir at T C ¼ 400 K.
T H p = 12 bar
Temperature, T
2
p = 1 bar
1
T
C
Specific entropy, s
FIGURE P6.3
Temperature-entropy diagram for Joule cyle.
1. Evaluate the Carnot efficiency and compare this with the Joule efficiency; explain why the
Joule efficiency is the lower.
2. Calculate the ratio of the gas turbine cycle work to the energy delivered from the high-
temperature reservoir (Q H for the Carnot cycle). This ratio is less than the Joule efficiency –
explain why in terms of unavailable energy.
3. Calculate the external irreversibilities and describe how these may be reduced to enable the
Joule efficiency to be achieved.
4. What are the mean temperatures of energy addition and rejection in the Joule cycle? What
would be the thermal efficiency of a Carnot cycle based on these mean temperatures?
[0.667; 0.508; 0.4212; I H /c p ¼ 79.9; 994 K; 489 K]