Page 169 - Advanced Thermodynamics for Engineers, Second Edition

156 CHAPTER 7 GENERAL THERMODYNAMIC RELATIONSHIPS

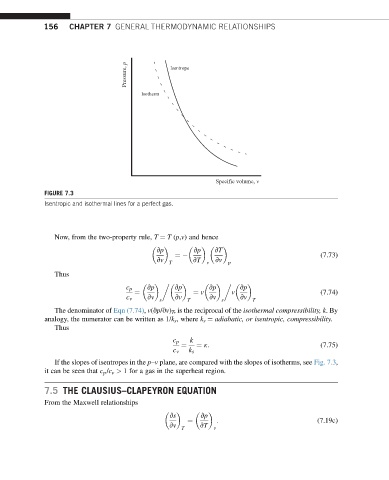
Pressure, p Isentrope

Isotherm

Specific volume, v
FIGURE 7.3
Isentropic and isothermal lines for a perfect gas.

Now, from the two-property rule, T ¼ T (p,v) and hence

vp vp vT
¼ (7.73)
vv vT vv
T v p
Thus

c p vp vp vp vp
¼ ¼ v v (7.74)
c v vv s vv T vv s vv T
The denominator of Eqn (7.74), v(vp/vv) T , is the reciprocal of the isothermal compressibility, k.By
analogy, the numerator can be written as 1/k s , where k s ¼ adiabatic, or isentropic, compressibility.
Thus
k
c p
¼ ¼ k: (7.75)
c v k s
If the slopes of isentropes in the p–v plane, are compared with the slopes of isotherms, see Fig. 7.3,
it can be seen that c p /c v > 1 for a gas in the superheat region.

7.5 THE CLAUSIUS–CLAPEYRON EQUATION
From the Maxwell relationships

vs vp
¼ : (7.19c)
vv vT
T v