Page 535 - Advanced engineering mathematics

15.1 Eigenfunction Expansions 515

1

0.8

0.6

0.4

0.2

0
0 0.2 0.4 0.6 0.8 1
x
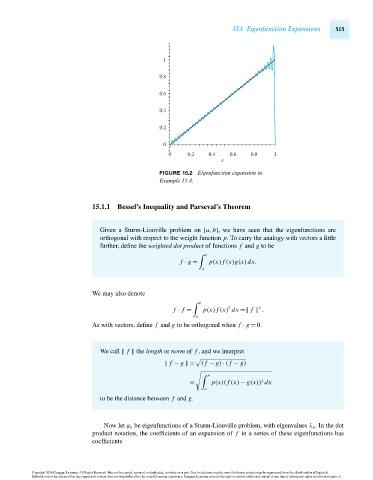
FIGURE 15.2 Eigenfunction expansion in
Example 15.4.

15.1.1 Bessel’s Inequality and Parseval’s Theorem

Given a Sturm-Liouville problem on [a,b], we have seen that the eigenfunctions are
orthogonal with respect to the weight function p. To carry the analogy with vectors a little
further, define the weighted dot product of functions f and g to be
b
f · g = p(x) f (x)g(x)dx.
a

We may also denote
b
2
2
f · f = p(x) f (x) dx = f .
a
As with vectors, define f and g to be orthogonal when f · g = 0.

We call f the length or norm of f , and we interpret

f − g = ( f − g) · ( f − g)

b
2
= p(x)( f (x) − g(x)) dx
a
to be the distance between f and g.

Now let ϕ n be eigenfunctions of a Sturm-Liouville problem, with eigenvalues λ n . In the dot
product notation, the coefficients of an expansion of f in a series of these eigenfunctions has
coefficients

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 15:20 THM/NEIL Page-515 27410_15_ch15_p505-562