Page 123 - Air pollution and greenhouse gases from basic concepts to engineering applications for air emission control

4.2 Rectilinear Particle Motion 97

This equation shows that when t approaches infinity, the settling speed of the
aerosol particle approaches a constant, which is the maximum speed that the par-
ticle can reach. In aerosol dynamics, this maximum speed is called terminal setting
velocity, denoted by v TS .
2
q d gC c
p p
v TS ¼ vðt !1Þ¼ gs ¼ ð4:20Þ
18l
Then Eq. (4.19) can be simplified as

vðtÞ t
¼ 1 exp ð4:21Þ
v TS s

This equation gives the speed vðtÞ of a particle at any time t after it is released in
still air in a gravitational field.
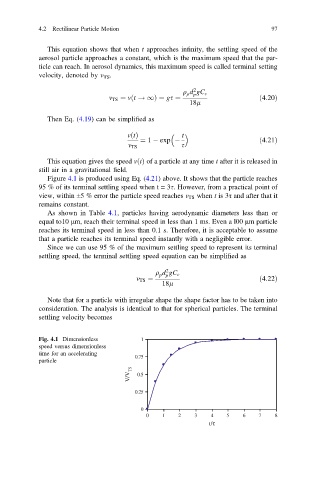
Figure 4.1 is produced using Eq. (4.21) above. It shows that the particle reaches
95 % of its terminal settling speed when t = 3s. However, from a practical point of
view, within ±5 % error the particle speed reaches v TS when t is 3τ and after that it
remains constant.
As shown in Table 4.1, particles having aerodynamic diameters less than or
equal to10 μm, reach their terminal speed in less than 1 ms. Even a l00 μm particle
reaches its terminal speed in less than 0.1 s. Therefore, it is acceptable to assume
that a particle reaches its terminal speed instantly with a negligible error.
Since we can use 95 % of the maximum settling speed to represent its terminal
settling speed, the terminal settling speed equation can be simplified as

2
q d gC c
p p
v TS ¼ ð4:22Þ
18l
Note that for a particle with irregular shape the shape factor has to be taken into
consideration. The analysis is identical to that for spherical particles. The terminal
settling velocity becomes

Fig. 4.1 Dimensionless 1
speed versus dimensionless
time for an accelerating
0.75
particle
V/V TS 0.5

0.25

0
0 1 2 3 4 5 6 7 8
t/τ