Page 213 - Air pollution and greenhouse gases from basic concepts to engineering applications for air emission control

188 6 Separation of Particles from a Gas

4H ij
N vdw ¼ ð6:113Þ
2
9pld U 0
p
where H ij = Hamaker constant that characterizes the interaction between aerosol
particles and the granule. In general, the Hamaker constant is case-specific and it
quantifies the interaction between the airborne particles and the fluids [2]. Three
example constants are listed in Table 6.2. Much more of the Hamaker constants of
inorganic materials can be found in the paper by Bergstrom [2].
Later on, Tufenkji and Elimelech [35] further improved the granular filtration
model by including interception in the simulation of particle motion. The single
granule collection efficiency by this new model is described as

0:081 15
1 d p 1 d p 8
g sG ¼ 2:4A sPe 0:715 N 0:052 þ 0:55A s N A 8
3
vdw
d G d G
ð6:114Þ
0:24

0:053
þ 0:22N vdw Gr 1:11 d p
d G
where Pe is the particle Peclet number (Pe) and N A is the attraction number that
characterizes the effects of van der Walls attraction and fluid velocity on particle
deposition due to interception.
H ij
N A ¼ ð6:115Þ
2
3pld U 0
p
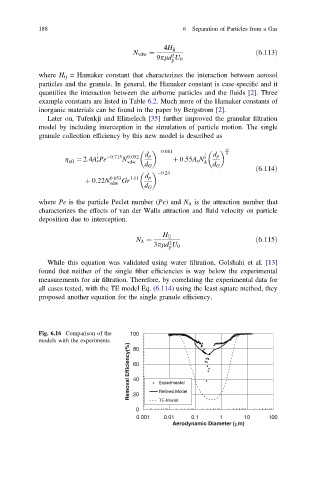
While this equation was validated using water filtration, Golshahi et al. [13]
found that neither of the single fiber efficiencies is way below the experimental
measurements for air filtration. Therefore, by correlating the experimental data for
all cases tested, with the TE model Eq. (6.114) using the least square method, they
proposed another equation for the single granule efficiency,

Fig. 6.16 Comparison of the 100
models with the experiments 80
Removal Efficiency(%) 60 Experimental

40

20
TE-Model
0 Refined Model
0.001 0.01 0.1 1 10 100
μ
Aerodynamic Diameter ( m)