Page 173 - Aircraft Stuctures for Engineering Student

6.2 Inelastic buckling 157

E
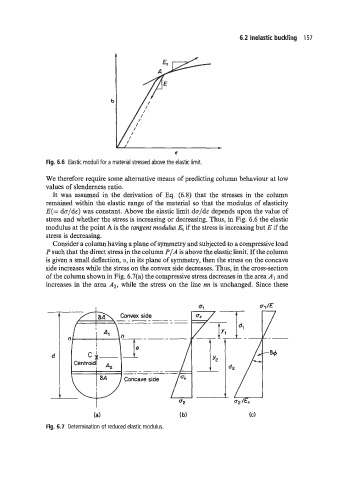
Fig. 6.6 Elastic moduli for a material stressed above the elastic limit.

We therefore require some alternative means of predicting column behaviour at low
values of slenderness ratio.
It was assumed in the derivation of Eq. (6.8) that the stresses in the column
remained within the elastic range of the material so that the modulus of elasticity
E(= dc/da) was constant. Above the elastic limit da/de depends upon the value of
stress and whether the stress is increasing or decreasing. Thus, in Fig. 6.6 the elastic
modulus at the point A is the tangent rnoduhs Et if the stress is increasing but E if the
stress is decreasing.
Consider a column having a plane of symmetry and subjected to a compressive load
P such that the direct stress in the column PIA is above the elastic limit. If the column
is given a small deflection, v, in its plane of symmetry, then the stress on the concave
side increases while the stress on the convex side decreases. Thus, in the cross-section
of the column shown in Fig. 6.7(a) the compressive stress decreases in the area A, and
increases in the area A2, while the stress on the line nn is unchanged. Since these

(a) (b)
Fig. 6.7 Determination of reduced elastic modulus.