Page 34 - Applied Numerical Methods Using MATLAB

BASIC OPERATIONS OF MATLAB 23
1. Random Number Having Uniform Distribution
The numbers in a matrix generated by the MATLAB function rand(M,N) have
uniform probability distribution over the interval [0,1], as described by U(0,1).
The random number x generated by rand() has the probability density function

1 ∀x ≥ 0
f X (x) = u s (x) − u s (x − 1) (u s (x) = : the unit step function)
0 ∀x< 0
(1.1.1)
whose value is 1 over [0,1] and 0 elsewhere. The average of this standard uniform
number x is
1
∞

1 2
x 1
m X = xf X (x)dx = xdx = = (1.1.2)
−∞ 0 2 0 2
and its variance or deviation is

1 1
∞ 1 1 1
2 2 2 1
σ = (x − m X ) f X (x)dx = (x − ) dx = (x − ) 3 =
X 2 3 2 12
−∞ 0 0
(1.1.3)
If you want another random number y with uniform distribution U(a, b), trans-
form the standard uniform number x as follows:
y = (b − a)x + a (1.1.4)
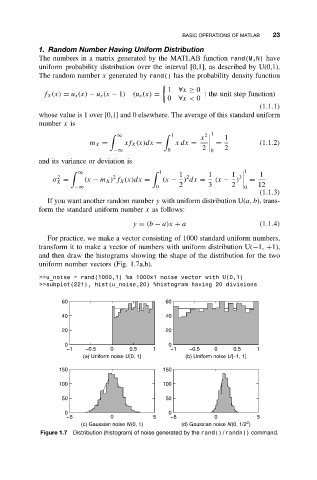
For practice, we make a vector consisting of 1000 standard uniform numbers,
transform it to make a vector of numbers with uniform distribution U(−1, +1),
and then draw the histograms showing the shape of the distribution for the two
uniform number vectors (Fig. 1.7a,b).

>>u_noise = rand(1000,1) %a 1000x1 noise vector with U(0,1)
>>subplot(221), hist(u_noise,20) %histogram having 20 divisions

60 60
40 40

20 20
0 0
−1 −0.5 0 0.5 1 −1 −0.5 0 0.5 1
(a) Uniform noise U[0, 1] (b) Uniform noise U[−1, 1]

150 150
100 100

50 50
0 0
−5 0 5 −5 0 5
2
(c) Gaussian noise N(0, 1) (d) Gaussian noise N(0, 1/2 )
Figure 1.7 Distribution (histogram) of noise generated by the rand()/randn() command.