Page 230 - Autonomous Mobile Robots

Stabilization of Nonholonomic Systems 215

2.5

2

1.5
1

0.5

0

– 0.5
– 1

– 1.5
– 0.5 0 0.5 1 1.5 2 2.5 3 3.5

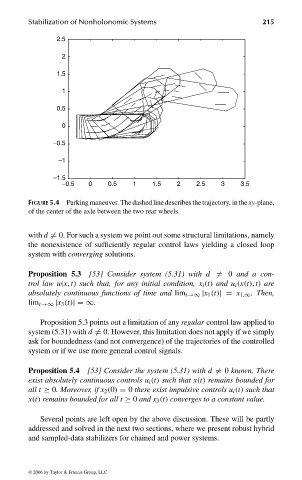
FIGURE 5.4 Parking maneuver. The dashed line describes the trajectory, in the xy-plane,
of the center of the axle between the two rear wheels.

with d = 0. For such a system we point out some structural limitations, namely
the nonexistence of sufficiently regular control laws yielding a closed loop
system with converging solutions.

Proposition 5.3 [53] Consider system (5.31) with d = 0 and a con-
trol law u(x, t) such that, for any initial condition, x i (t) and u i (x(t), t) are
absolutely continuous functions of time and lim t→∞ |x 1 (t)|= x 1,∞ . Then,
lim t→∞ |x 3 (t)|=∞.

Proposition 5.3 points out a limitation of any regular control law applied to
system (5.31) with d = 0. However, this limitation does not apply if we simply
ask for boundedness (and not convergence) of the trajectories of the controlled
system or if we use more general control signals.

Proposition 5.4 [53] Consider the system (5.31) with d = 0 known. There
exist absolutely continuous controls u i (t) such that x(t) remains bounded for
all t ≥ 0. Moreover, if x 2 (0) = 0 there exist impulsive controls u i (t) such that
x(t) remains bounded for all t ≥ 0 and x 3 (t) converges to a constant value.

Several points are left open by the above discussion. These will be partly
addressed and solved in the next two sections, where we present robust hybrid
and sampled-data stabilizers for chained and power systems.

© 2006 by Taylor & Francis Group, LLC

FRANKL: “dk6033_c005” — 2006/3/31 — 16:42 — page 215 — #29