Page 37 - Calc for the Clueless

Finally we will learn, sadly, that most integrals cannot be done. As we go on in math, we will learn many
approximation methods. Also, we will learn how accurate these approximations are. This is OK because we
don't live in a perfect world—or is this a surprise to you? As we go on, the methods of approximation will
become more involved. Let us take a look at some crude ones. We will approximate

in three ways.

Example 33—

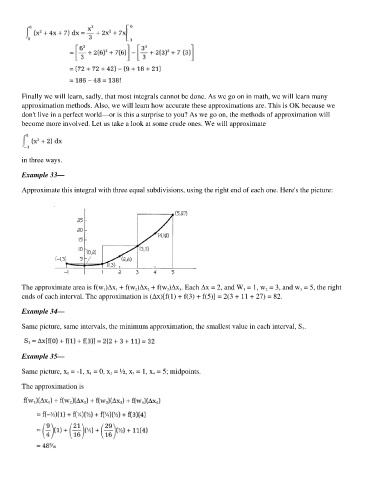
Approximate this integral with three equal subdivisions, using the right end of each one. Here's the picture:

The approximate area is f(w 1)∆x 1 + f(w 2)∆x 2 + f(w 3)∆x 3. Each ∆x = 2, and W 1 = 1, w 2 = 3, and w 3 = 5, the right
ends of each interval. The approximation is (∆x)[f(1) + f(3) + f(5)] = 2(3 + 11 + 27) = 82.

Example 34—

Same picture, same intervals, the minimum approximation, the smallest value in each interval, S 3.

Example 35—

Same picture, x 0 = -1, x 1 = 0, x 2 = ½, x 3 = 1, x 4 = 5; midpoints.

The approximation is