Page 50 - Calc for the Clueless

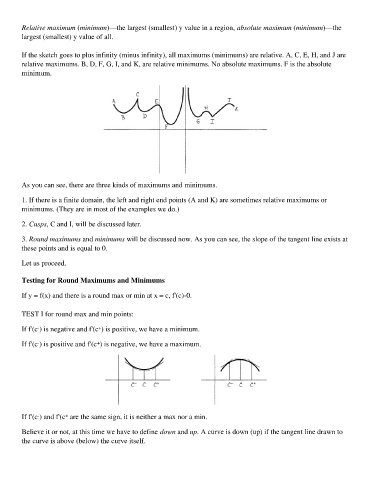
Relative maximum (minimum)—the largest (smallest) y value in a region, absolute maximum (minimum)—the
largest (smallest) y value of all.

If the sketch goes to plus infinity (minus infinity), all maximums (minimums) are relative. A, C, E, H, and J are
relative maximums. B, D, F, G, I, and K, are relative minimums. No absolute maximums. F is the absolute
minimum.

As you can see, there are three kinds of maximums and minimums.

1. If there is a finite domain, the left and right end points (A and K) are sometimes relative maximums or
minimums. (They are in most of the examples we do.)

2. Cusps, C and I, will be discussed later.

3. Round maximums and minimums will be discussed now. As you can see, the slope of the tangent line exists at
these points and is equal to 0.

Let us proceed.

Testing for Round Maximums and Minimums

If y = f(x) and there is a round max or min at x = c, f'(c)-0.

TEST I for round max and min points:

-
+
If f'(c ) is negative and f'(c ) is positive, we have a minimum.
-
If f'(c ) is positive and f'(c ) is negative, we have a maximum.
+

+
-
If f'(c ) and f'(c are the same sign, it is neither a max nor a min.
Believe it or not, at this time we have to define down and up. A curve is down (up) if the tangent line drawn to
the curve is above (below) the curve itself.