Page 73 - Calculus for the Clueless, Calc II

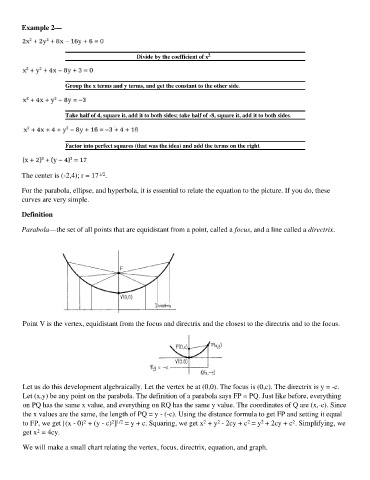
Example 2—

Divide by the coefficient of x 2

Group the x terms and y terms, and get the constant to the other side.

Take half of 4, square it, add it to both sides; take half of -8, square it, add it to both sides.

Factor into perfect squares (that was the idea) and add the terms on the right.

The center is (-2,4); r = 17 .
1/2
For the parabola, ellipse, and hyperbola, it is essential to relate the equation to the picture. If you do, these
curves are very simple.

Definition

Parabola—the set of all points that are equidistant from a point, called a focus, and a line called a directrix.

Point V is the vertex, equidistant from the focus and directrix and the closest to the directrix and to the focus.

Let us do this development algebraically. Let the vertex be at (0,0). The focus is (0,c). The directrix is y = -c.
Let (x,y) be any point on the parabola. The definition of a parabola says FP = PQ. Just like before, everything
on PQ has the same x value, and everything on RQ has the same y value. The coordinates of Q are (x,-c). Since
the x values are the same, the length of PQ = y - (-c). Using the distance formula to get FP and setting it equal
to FP, we get [(x - 0) + (y - c) ] = y + c. Squaring, we get x + y - 2cy + c = y + 2cy + c . Simplifying, we
2 1/2
2
2
2
2
2
2
get x = 4cy.
2
We will make a small chart relating the vertex, focus, directrix, equation, and graph.