Page 368 - Civil Engineering Formulas

HYDRAULICS AND WATERWORKS FORMULAS 297

Total energy per lb of liquid
2
V g
2g

P
P a Elemental volume
w
w of liquid
V a

Velocity
distribution
ZZ a

Arbitrary datum plane

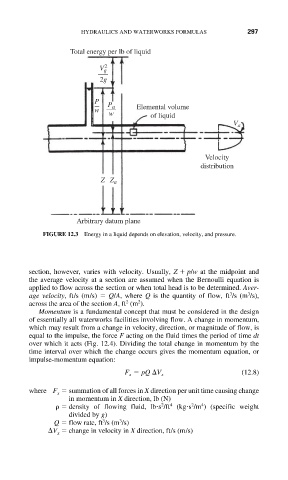
FIGURE 12.3 Energy in a liquid depends on elevation, velocity, and pressure.

section, however, varies with velocity. Usually, Z p/w at the midpoint and
the average velocity at a section are assumed when the Bernoulli equation is
applied to flow across the section or when total head is to be determined. Aver-
3
3
age velocity, ft/s (m/s) Q/A, where Q is the quantity of flow, ft /s (m /s),
2
2
across the area of the section A, ft (m ).
Momentum is a fundamental concept that must be considered in the design
of essentially all waterworks facilities involving flow. A change in momentum,
which may result from a change in velocity, direction, or magnitude of flow, is
equal to the impulse, the force F acting on the fluid times the period of time dt
over which it acts (Fig. 12.4). Dividing the total change in momentum by the
time interval over which the change occurs gives the momentum equation, or
impulse-momentum equation:
(12.8)
F x pQ V x
where F summation of all forces in X direction per unit time causing change
x
in momentum in X direction, lb (N)
2
4
4
2
density of flowing fluid, lb s /ft (kg s /m ) (specific weight
divided by g)
3
3
Q flow rate, ft /s (m /s)
V change in velocity in X direction, ft/s (m/s)
x