Page 375 - Civil Engineering Formulas

304 CHAPTER TWELVE

For pipes flowing full:
S
V 0.55C 1 D 0.63 0.54 (12.29)
S
Q 0.432C 1 D 2.63 0.54 (12.30)
4.727 Q 1.85
L
h f 4.87 (12.31)
D C 1
1.376 Q 0.38
D 0.205 (12.32)
S C 1
where V velocity, ft/s (m/s)
C coefficient, dependent on surface roughness (given in engineering
1
handbooks)
R hydraulic radius, ft (m)
S head loss due to friction, ft/ft (m/m) of pipe
D diameter of pipe, ft (m)
L length of pipe, ft (m)
3
3
Q discharge, ft /s (m /s)
h friction loss, ft (m)
f
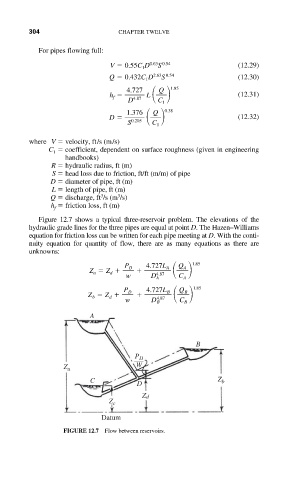
Figure 12.7 shows a typical three-reservoir problem. The elevations of the
hydraulic grade lines for the three pipes are equal at point D. The Hazen–Williams
equation for friction loss can be written for each pipe meeting at D. With the conti-
nuity equation for quantity of flow, there are as many equations as there are
unknowns:
4.87
Z a Z d P D 4.727L A Q A 1.85
w D A C A
4.87
P D 4.727L B Q B 1.85
Z b Z d
w D B C B
A

B
P D
Z a W

C Z b
D
Zd
Z c
Datum
FIGURE 12.7 Flow between reservoirs.