Page 38 - Computational Modeling in Biomedical Engineering and Medical Physics

24 Computational Modeling in Biomedical Engineering and Medical Physics

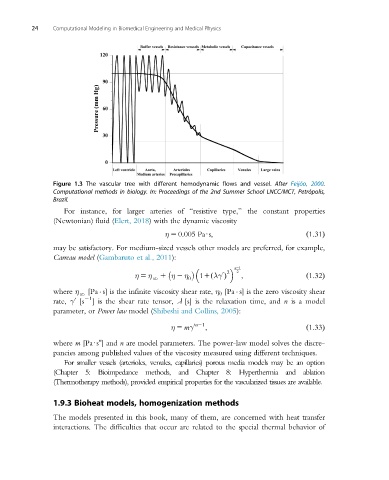
Figure 1.3 The vascular tree with different hemodynamic flows and vessel. After Feijóo, 2000.
Computational methods in biology. In: Proceedings of the 2nd Summer School LNCC/MCT, Petrópolis,
Brazil.
For instance, for larger arteries of “resistive type,” the constant properties
(Newtonian) fluid (Elert, 2018) with the dynamic viscosity
η 5 0:005 PaUs; ð1:31Þ
may be satisfactory. For medium-sized vessels other models are preferred, for example,
Carreau model (Gambaruto et al., 2011):
n21

η 5 η 1 η 2 η 0 11 λγ Þ 2 ; ð1:32Þ
0 2

ð
N
where η N [Pa s] is the infinite viscosity shear rate, η 0 [Pa s] is the zero viscosity shear
0
rate, γ [s 21 ] is the shear rate tensor, λ [s] is the relaxation time, and n is a model
parameter, or Power law model (Shibeshi and Collins, 2005):
η 5 mγ 0n21 ; ð1:33Þ
n
where m [PaUs ] and n are model parameters. The power-law model solves the discre-
pancies among published values of the viscosity measured using different techniques.
For smaller vessels (arterioles, venules, capillaries) porous media models may be an option
(Chapter 5: Bioimpedance methods, and Chapter 8: Hyperthermia and ablation
(Thermotherapy methods), provided empirical properties for the vascularized tissues are available.

1.9.3 Bioheat models, homogenization methods

The models presented in this book, many of them, are concerned with heat transfer
interactions. The difficulties that occur are related to the special thermal behavior of