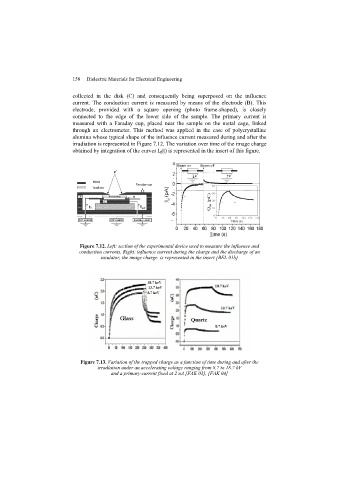
Page 170 - Discrete Mathematics and Its Applications

2.3 Functions 149

DEFINITION 12 The floor function assigns to the real number x the largest integer that is less than or equal to
x. The value of the floor function at x is denoted by x . The ceiling function assigns to the
real number x the smallest integer that is greater than or equal to x. The value of the ceiling
function at x is denoted by x .

Remark: The floor function is often also called the greatest integer function. It is often denoted
by [x].

EXAMPLE 26 These are some values of the floor and ceiling functions:

1
1
1
1
= 0, = 1, − =−1, − = 0, 3.1 = 3, 3.1 = 4, 7 = 7, 7 = 7. ▲
2 2 2 2
We display the graphs of the floor and ceiling functions in Figure 10. In Figure 10(a) we display
the graph of the floor function x . Note that this function has the same value throughout the
interval [n, n + 1), namely n, and then it jumps up to n + 1 when x = n + 1. In Figure 10(b)
we display the graph of the ceiling function x . Note that this function has the same value
throughout the interval (n, n + 1], namely n + 1, and then jumps to n + 2 when x is a little
larger than n + 1.
The floor and ceiling functions are useful in a wide variety of applications, including those
involving data storage and data transmission. Consider Examples 27 and 28, typical of basic
calculations done when database and data communications problems are studied.

EXAMPLE 27 Data stored on a computer disk or transmitted over a data network are usually represented as a
string of bytes. Each byte is made up of 8 bits. How many bytes are required to encode 100 bits
of data?

Solution: To determine the number of bytes needed, we determine the smallest integer that is at
least as large as the quotient when 100 is divided by 8, the number of bits in a byte. Consequently,
100/8 = 12.5 = 13 bytes are required. ▲

EXAMPLE 28 In asynchronous transfer mode (ATM) (a communications protocol used on backbone networks),
data are organized into cells of 53 bytes. How many ATM cells can be transmitted in 1 minute
over a connection that transmits data at the rate of 500 kilobits per second?

Solution: In 1 minute, this connection can transmit 500,000 · 60 = 30,000,000 bits. Each ATM
cell is 53 bytes long, which means that it is 53 · 8 = 424 bits long. To determine the number

3 3

2 2
1 1

–3 –2 –1 1 2 3 –3 –2 –1 1 2 3
–1 –1
–2 –2

–3 –3
(a) y = x (b) y = x

FIGURE 10 Graphs of the (a) Floor and (b) Ceiling Functions.