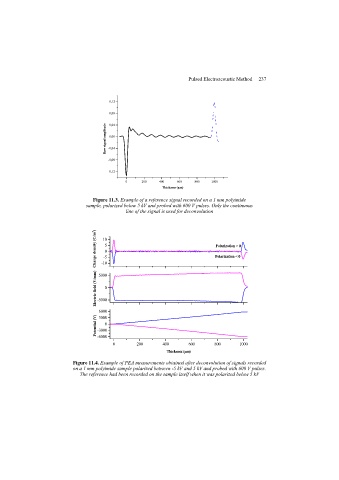
Page 247 - Discrete Mathematics and Its Applications

226 3 / Algorithms

TABLE 1 Commonly Used Terminology for the
Complexity of Algorithms.
Complexity Terminology
(1) Constant complexity
(log n) Logarithmic complexity
(n) Linear complexity
(n log n) Linearithmic complexity
b
(n ) Polynomial complexity
n
(b ), where b> 1 Exponential complexity
(n!) Factorial complexity

b
An algorithm has polynomial complexity if it has complexity (n ), where b is an integer
with b ≥ 1. For example, the bubble sort algorithm is a polynomial-time algorithm because
2
it uses (n ) comparisons in the worst case. An algorithm has exponential complexity if it
n
has time complexity (b ), where b> 1. The algorithm that determines whether a compound
proposition in n variables is satisfiable by checking all possible assignments of truth variables
n
is an algorithm with exponential complexity, because it uses (2 ) operations. Finally, an
algorithm has factorial complexity if it has (n!) time complexity. The algorithm that finds all
orders that a traveling salesperson could use to visit n cities has factorial complexity; we will
discuss this algorithm in Chapter 9.

TRACTABILITY A problem that is solvable using an algorithm with polynomial worst-case
complexity is called tractable, because the expectation is that the algorithm will produce the
solution to the problem for reasonably sized input in a relatively short time. However, if the
polynomial in the big- estimate has high degree (such as degree 100) or if the coefficients
are extremely large, the algorithm may take an extremely long time to solve the problem.
Consequently, that a problem can be solved using an algorithm with polynomial worst-case
time complexity is no guarantee that the problem can be solved in a reasonable amount of time
for even relatively small input values. Fortunately, in practice, the degree and coefficients of
polynomials in such estimates are often small.
The situation is much worse for problems that cannot be solved using an algorithm with
worst-case polynomial time complexity. Such problems are called intractable. Usually, but not
always, an extremely large amount of time is required to solve the problem for the worst cases
of even small input values. In practice, however, there are situations where an algorithm with a
certain worst-case time complexity may be able to solve a problem much more quickly for most
cases than for its worst case. When we are willing to allow that some, perhaps small, number
of cases may not be solved in a reasonable amount of time, the average-case time complexity is
a better measure of how long an algorithm takes to solve a problem. Many problems important
in industry are thought to be intractable but can be practically solved for essentially all sets of
input that arise in daily life. Another way that intractable problems are handled when they arise
in practical applications is that instead of looking for exact solutions of a problem, approximate
solutions are sought. It may be the case that fast algorithms exist for finding such approximate so-
lutions,perhapsevenwithaguaranteethattheydonotdifferbyverymuchfromanexactsolution.
Some problems even exist for which it can be shown that no algorithm exists for solving
them. Such problems are called unsolvable (as opposed to solvable problems that can be
solved using an algorithm). The first proof that there are unsolvable problems was provided by
the great English mathematician and computer scientist Alan Turing when he showed that the
halting problem is unsolvable. Recall that we proved that the halting problem is unsolvable in
Section 3.1. (A biography of Alan Turing and a description of some of his other work can be
found in Chapter 13.)