Page 321 - Discrete Mathematics and Its Applications

300 4 / Number Theory and Cryptography
EXAMPLE 8
Example 8 illustrates how RSA encryption is performed. For practical reasons we use small
primes p and q in this example, rather than primes with 200 or more digits. Although the cipher
described in this example is not secure, it does illustrate the techniques used in the RSA cipher.
Encrypt the message STOP using the RSA cryptosystem with key (2537, 13). Note that 2537 =
43 · 59, p = 43 and q = 59 are primes, and
gcd(e, (p − 1)(q − 1)) = gcd(13, 42 · 58) = 1.
Solution: To encrypt, we first translate the letters in STOP into their numerical equivalents. We
then group these numbers into blocks of four digits (because 2525 < 2537 < 252525), to obtain
1819 1415.
We encrypt each block using the mapping
C = M 13 mod 2537.
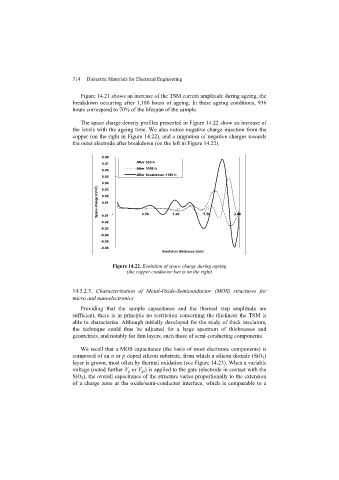
Computations using fast modular multiplication show that 1819 13 mod 2537 = 2081 and
1415 13 mod 2537 = 2182. The encrypted message is 2081 2182. ▲
RSA Decryption
The plaintext message can be quickly recovered from a ciphertext message when the decryp-
tion key d, an inverse of e modulo (p − 1)(q − 1), is known. [Such an inverse exists because
gcd(e, (p − 1)(q − 1)) = 1.] To see this, note that if de ≡ 1 (mod (p − 1)(q − 1)), there is an
integer k such that de = 1 + k(p − 1)(q − 1). It follows that
d
e d
C ≡ (M ) = M de = M 1+k(p−1)(q−1) (mod n).
RONALD RIVEST (BORN 1948) Ronald Rivest received a B.A. fromYale in 1969 and his Ph.D. in computer
science from Stanford in 1974. Rivest is a computer science professor at M.I.T. and was a cofounder of RSA Data
Security, which held the patent on the RSA cryptosystem that he invented together withAdi Shamir and Leonard
Adleman. Areas that Rivest has worked in besides cryptography include machine learning, VLSI design, and
computer algorithms. He is a coauthor of a popular text on algorithms ([CoLeRiSt09]).
ADI SHAMIR (BORN 1952) Adi Shamir was born in Tel Aviv, Israel. His undergraduate degree is from
Tel Aviv University (1972) and his Ph.D. is from the Weizmann Institute of Science (1977). Shamir was a
research assistant at the University of Warwick and an assistant professor at M.I.T. He is currently a profes-
sor in the Applied Mathematics Department at the Weizmann Institute and leads a group studying computer
security. Shamir’s contributions to cryptography, besides the RSA cryptosystem, include cracking knapsack
cryptosystems, cryptanalysis of the Data Encryption Standard (DES), and the design of many cryptographic
protocols.
LEONARDADLEMAN (BORN 1945) LeonardAdleman was born in San Francisco, California. He received
a B.S. in mathematics (1968) and his Ph.D. in computer science (1976) from the University of California,
Berkeley. Adleman was a member of the mathematics faculty at M.I.T. from 1976 until 1980, where he was
a coinventor of the RSA cryptosystem, and in 1980 he took a position in the computer science department at
the University of Southern California (USC). He was appointed to a chaired position at USC in 1985. Adleman
has worked on computer security, computational complexity, immunology, and molecular biology. He invented
the term “computer virus.” Adleman’s recent work on DNA computing has sparked great interest. He was a
technical adviser for the movie Sneakers, in which computer security played an important role.