Page 344 - Discrete Mathematics and Its Applications

5.1 Mathematical Induction 323

•
a
X
T

X
S

X {a}
a •
T

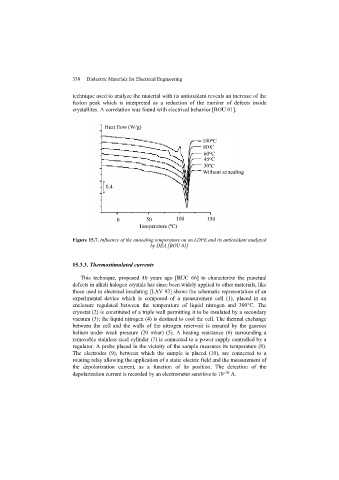
FIGURE 3 Generating Subsets of a Set with k + 1 Elements. Here T = S ∪{a}.

EXAMPLE 10 The Number of Subsets of a Finite Set Use mathematical induction to show that if S is a
n
finite set with n elements, where n is a nonnegative integer, then S has 2 subsets. (We will
prove this result directly in several ways in Chapter 6.)
n
Solution: Let P (n) be the proposition that a set with n elements has 2 subsets.
0
BASIS STEP: P(0) is true, because a set with zero elements, the empty set, has exactly 2 = 1
subset, namely, itself.
INDUCTIVE STEP: For the inductive hypothesis we assume that P(k) is true for an arbitrary
k
nonnegative integer k, that is, we assume that every set with k elements has 2 subsets. It must
be shown that under this assumption, P(k + 1), which is the statement that every set with k + 1
elements has 2 k+1 subsets, must also be true. To show this, let T be a set with k + 1 elements.
Then, it is possible to write T = S ∪{a}, where a is one of the elements of T and S = T −{a}
(and hence |S|= k). The subsets of T can be obtained in the following way. For each subset X
of S there are exactly two subsets of T , namely, X and X ∪{a}. (This is illustrated in Figure 3.)
These constitute all the subsets of T and are all distinct. We now use the inductive hypothesis
k
to conclude that S has 2 subsets, because it has k elements. We also know that there are two
k
subsets of T for each subset of S. Therefore, there are 2 · 2 = 2 k+1 subsets of T . This finishes
the inductive argument.
Because we have completed the basis step and the inductive step, by mathematical induction
it follows that P (n) is true for all nonnegative integers n. That is, we have proved that a set
n
with n elements has 2 subsets whenever n is a nonnegative integer. ▲
EXAMPLE 11 Use mathematical induction to prove the following generalization of one of De Morgan’s laws:

n n

A j = A j
j = 1 j = 1

whenever A 1 ,A 2 ,...,A n are subsets of a universal set U and n ≥ 2.

Solution: Let P(n) be the identity for n sets.
BASIS STEP: The statement P(2) asserts that A 1 ∩ A 2 = A 1 ∪ A 2 . This is one of De Morgan’s
laws; it was proved in Example 11 of Section 2.2.