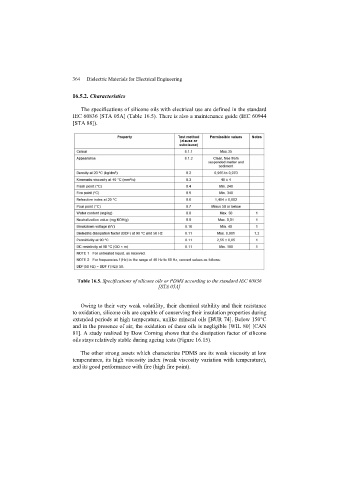
Page 369 - Discrete Mathematics and Its Applications

348 5 / Induction and Recursion

Proof: Recall that when the Euclidean algorithm is applied to find gcd(a, b) with a ≥ b, this
sequence of equations (where a = r 0 and b = r 1 ) is obtained.

r 0 = r 1 q 1 + r 2 0 ≤ r 2 <r 1 ,

r 1 = r 2 q 2 + r 3 0 ≤ r 3 <r 2 ,
·
·
·
r n−2 = r n−1 q n−1 + r n 0 ≤ r n <r n−1 ,
r n−1 = r n q n .

Here n divisions have been used to find r n = gcd(a, b). Note that the quotients q 1 ,q 2 ,...,q n−1
are all at least 1. Moreover, q n ≥ 2, because r n <r n−1 . This implies that

r n ≥ 1 = f 2 ,

r n−1 ≥ 2r n ≥ 2f 2 = f 3 ,
r n−2 ≥ r n−1 + r n ≥ f 3 + f 2 = f 4 ,
·
·
·
r 2 ≥ r 3 + r 4 ≥ f n−1 + f n−2 = f n ,

b = r 1 ≥ r 2 + r 3 ≥ f n + f n−1 = f n+1 .

It follows that if n divisions are used by the Euclidean algorithm to find gcd(a, b) with a ≥ b,
√
then b ≥ f n+1 . By Example 4 we know that f n+1 >α n−1 for n> 2, where α = (1 + 5)/2.
Therefore, it follows that b> α n−1 . Furthermore, because log α ≈ 0.208 > 1/5, we see that
10

log b> (n − 1) log α> (n − 1)/5.
10
10
k
Hence, n − 1 < 5 · log b. Now suppose that b has k decimal digits. Then b< 10 and
10
log b< k. It follows that n − 1 < 5k, and because k is an integer, it follows that n ≤ 5k.
10
This finishes the proof.
Because the number of decimal digits in b, which equals log b + 1, is less than or equal
10
to log b + 1, Theorem 1 tells us that the number of divisions required to find gcd(a, b) with
10

FIBONACCI (1170–1250) Fibonacci (short for filius Bonacci, or “son of Bonacci”) was also known as
Leonardo of Pisa. He was born in the Italian commercial center of Pisa. Fibonacci was a merchant who traveled
extensively throughout the Mideast, where he came into contact with Arabian mathematics. In his book Liber
Abaci, Fibonacci introduced the European world to Arabic notation for numerals and algorithms for arithmetic.
It was in this book that his famous rabbit problem (described in Section 8.1) appeared. Fibonacci also wrote
books on geometry and trigonometry and on Diophantine equations, which involve finding integer solutions to
equations.