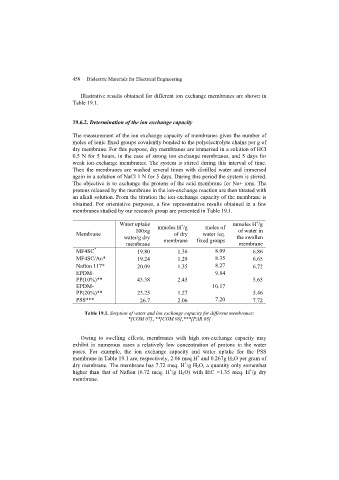
Page 461 - Discrete Mathematics and Its Applications

440 6 / Counting

c) How can the product rule be used to find the number 13. a) Explain how to find a formula for the number of ways
of one-to-one functions from a set with m elements to to select r objects from n objects when repetition is
a set with n elements? allowed and order does not matter.
d) How many one-to-one functions are there from a set b) How many ways are there to select a dozen objects
with five elements to a set with 10 elements? from among objects of five different types if objects
e) How many onto functions are there from a set with of the same type are indistinguishable?
five elements to a set with 10 elements? c) How many ways are there to select a dozen objects
4. How can you find the number of possible outcomes of a from these five different types if there must be at least
playoff between two teams where the first team that wins three objects of the first type?
four games wins the playoff? d) How many ways are there to select a dozen objects
5. How can you find the number of bit strings of length ten from these five different types if there cannot be more
that either begin with 101 or end with 010? than four objects of the first type?
6. a) State the pigeonhole principle. e) How many ways are there to select a dozen objects
b) Explain how the pigeonhole principle can be used to from these five different types if there must be at least
show that among any 11 integers, at least two must two objects of the first type, but no more than three
have the same last digit. objects of the second type?
7. a) State the generalized pigeonhole principle. 14. a) Let n and r be positive integers. Explain why the
b) Explain how the generalized pigeonhole principle can number of solutions of the equation x 1 + x 2 + ···+
be used to show that among any 91 integers, there are x n = r, where x i is a nonnegative integer for i =
at least ten that end with the same digit. 1, 2, 3,...,n, equals the number of r-combinations
8. a) What is the difference between an r-combination and of a set with n elements.
an r-permutation of a set with n elements? b) How many solutions in nonnegative integers are there
b) Derive an equation that relates the number of r-com- to the equation x 1 + x 2 + x 3 + x 4 = 17?
binations and the number of r-permutations of a set c) How many solutions in positive integers are there to
with n elements. the equation in part (b)?
c) How many ways are there to select six students from
a class of 25 to serve on a committee? 15. a) Derive a formula for the number of permutations of n
d) How many ways are there to select six students from objects of k different types, where there are n 1 indis-
a class of 25 to hold six different executive positions tinguishable objects of type one, n 2 indistinguishable
on a committee? objects of type two,..., and n k indistinguishable ob-
jects of type k.
9. a) What is Pascal’s triangle? b) How many ways are there to order the letters of the
b) How can a row of Pascal’s triangle be produced from word INDISCREETNESS?
the one above it?
16. Describe an algorithm for generating all the permutations
10. What is meant by a combinatorial proof of an identity?
How is such a proof different from an algebraic one? of the set of the n smallest positive integers.
11. Explain how to prove Pascal’s identity using a combina- 17. a) How many ways are there to deal hands of five cards
torial argument. to six players from a standard 52-card deck?
b) How many ways are there to distribute n distinguish-
12. a) State the binomial theorem.
b) Explain how to prove the binomial theorem using a able objects into k distinguishable boxes so that n i
objects are placed in box i?
combinatorial argument.
y
c) Find the coefficient of x 100 101 in the expansion of 18. Describe an algorithm for generating all the combinations
(2x + 5y) 201 . of the set of the n smallest positive integers.

Supplementary Exercises

1. How many ways are there to choose 6 items from 10 dis- 2. How many ways are there to choose 10 items from 6 dis-
tinct items when tinct items when
a) the items in the choices are ordered and repetition is a) the items in the choices are ordered and repetition is
not allowed? not allowed?
b) the items in the choices are ordered and repetition is b) the items in the choices are ordered and repetition is
allowed? allowed?
c) the items in the choices are unordered and repetition c) the items in the choices are unordered and repetition
is not allowed? is not allowed?
d) the items in the choices are unordered and repetition d) the items in the choices are unordered and repetition
is allowed? is allowed?