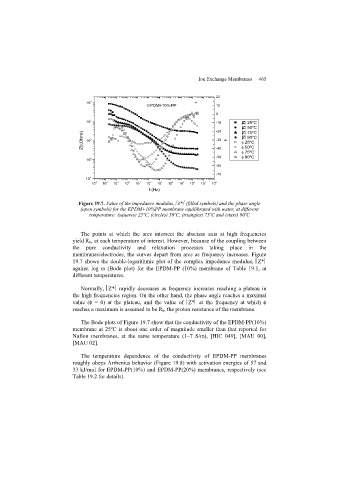
Page 468 - Discrete Mathematics and Its Applications

7.1 An Introduction to Discrete Probability 447

2
number of outcomes when two dice are rolled is 6 = 36.) There are six successful outcomes,
namely, (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), and (6, 1), where the values of the first and second
dice are represented by an ordered pair. Hence, the probability that a seven comes up when two
fair dice are rolled is 6/36 = 1/6. ▲

Lotteries are extremely popular throughout the world. We can easily compute the odds of
winning different types of lotteries, as illustrated in Examples 3 and 4. (The odd of winning the
popular Mega Millions and Powerball lotteries are studied in the supplementary exercises.)
EXAMPLE 3 In a lottery, players win a large prize when they pick four digits that match, in the correct order,
four digits selected by a random mechanical process. A smaller prize is won if only three digits
are matched. What is the probability that a player wins the large prize? What is the probability
that a player wins the small prize?

Solution: There is only one way to choose all four digits correctly. By the product rule, there
4
are 10 = 10,000 ways to choose four digits. Hence, the probability that a player wins the large
prize is 1/10,000 = 0.0001.
Players win the smaller prize when they correctly choose exactly three of the four digits.
Exactly one digit must be wrong to get three digits correct, but not all four correct. By the sum
rule, to find the number of ways to choose exactly three digits correctly, we add the number of
ways to choose four digits matching the digits picked in all but the ith position, for i = 1, 2, 3, 4.
To count the number of successes with the first digit incorrect, note that there are nine
possible choices for the first digit (all but the one correct digit), and one choice for each of the
other digits, namely, the correct digits for these slots. Hence, there are nine ways to choose four
digits where the first digit is incorrect, but the last three are correct. Similarly, there are nine
ways to choose four digits where the second digit is incorrect, nine with the third digit incorrect,
and nine with the fourth digit incorrect. Hence, there is a total of 36 ways to choose four digits
with exactly three of the four digits correct. Thus, the probability that a player wins the smaller
prize is 36/10,000 = 9/2500 = 0.0036. ▲

EXAMPLE 4 There are many lotteries now that award enormous prizes to people who correctly choose a set
of six numbers out of the first n positive integers, where n is usually between 30 and 60. What
is the probability that a person picks the correct six numbers out of 40?

Solution: There is only one winning combination. The total number of ways to choose six
numbers out of 40 is
40!
C(40, 6) = = 3,838,380.
34! 6!
Consequently, the probability of picking a winning combination is 1/3,838,380 ≈ 0.00000026.
(Here the symbol ≈ means approximately equal to.) ▲

PIERRE-SIMON LAPLACE (1749–1827) Pierre-Simon Laplace came from humble origins in Normandy.
In his childhood he was educated in a school run by the Benedictines. At 16 he entered the University of Caen
intending to study theology. However, he soon realized his true interests were in mathematics. After completing
his studies, he was named a provisional professor at Caen, and in 1769 he became professor of mathematics at
the Paris Military School.
Laplace is best known for his contributions to celestial mechanics, the study of the motions of heavenly bod-
ies. HisTraité de Mécanique Céleste is considered one of the greatest scientific works of the early nineteenth cen-
tury. Laplace was one of the founders of probability theory and made many contributions to mathematical statis-
tics. His work in this area is documented in his book Théorie Analytique des Probabilités, in which he defined
the probability of an event as the ratio of the number of favorable outcomes to the total number of outcomes of an experiment.
Laplace was famous for his political flexibility. He was loyal, in succession, to the French Republic, Napoleon, and King Louis
XVIII. This flexibility permitted him to be productive before, during, and after the French Revolution.