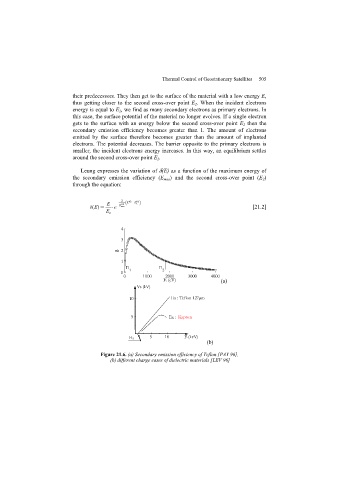
Page 507 - Discrete Mathematics and Its Applications

486 7 / Discrete Probability

Furthermore, p(X 1 = i) = 1/6 and p(X 2 = j) = 1/6, because the probability that i appears
on the first die and the probability that j appears on the second die are both 1/6. It follows that

1 1 1 1
p(X 1 = i and X 2 = j) = and p(X 1 = i)p(X 2 = j) = · = ,
36 6 6 36
so X 1 and X 2 are independent. ▲

EXAMPLE 12 Show that the random variables X 1 and X = X 1 + X 2 , where X 1 and X 2 are as defined in
Example 4, are not independent.

Solution: Note that p(X 1 = 1 and X = 12) = 0, because X 1 = 1 means the number appear-
ing on the first die is 1, which implies that the sum of the numbers appearing on the two
dice cannot equal 12. On the other hand, p(X 1 = 1) = 1/6 and p(X = 12) = 1/36. Hence
p(X 1 = 1 and X = 12) = p(X 1 = 1) · p(X = 12). This counterexample shows that X 1 and X
are not independent. ▲
The expected value of the product of two independent random variables is the product of
their expected values, as Theorem 5 shows.

THEOREM 5 IfX andY areindependentrandomvariablesonasamplespaceS,thenE(XY) = E(X)E(Y).

Proof: To prove this formula, we use the key observation that the event XY = r is the disjoint
union of the events X = r 1 and Y = r 2 over all r 1 ∈ X(S) and r 2 ∈ Y(S) with r = r 1 r 2 .We
have

E(XY) = r · p(XY = r) by Theorem 1
r∈XY(S)

= r 1 r 2 · p(X = r 1 and Y = r 2 ) expressing XY = r as a disjoint union
r 1 ∈X(S),r 2 ∈Y(S)

= r 1 r 2 · p(X = r 1 and Y = r 2 ) using a double sum to order the terms
r 1 ∈X(S) r 2 ∈Y(S)

= r 1 r 2 · p(X = r 1 ) · p(Y = r 2 ) by the independence of X and Y
r 1 ∈X(S) r 2 ∈Y(S)

= r 1 · p(X = r 1 ) · r 2 · p(Y = r 2 ) by factoring out r 1 · p(X = r 1 )
r 1 ∈X(S) r 2 ∈Y(S)

= r 1 · p(X = r 1 ) · E(Y) by the definition of E(Y)
r 1 ∈X(S)

= E(Y) r 1 · p(X = r 1 ) by factoring out E(Y)
r 1 ∈X(S)
= E(Y)E(X) by the definition of E(X)

We complete the proof by noting that E(Y)E(X) = E(X)E(Y), which is a consequence of the
commutative law for multiplication.

Note that when X and Y are random variables that are not independent, we cannot conclude
that E(XY) = E(X)E(Y), as Example 13 shows.