Page 645 - Discrete Mathematics and Its Applications

624 9 / Relations

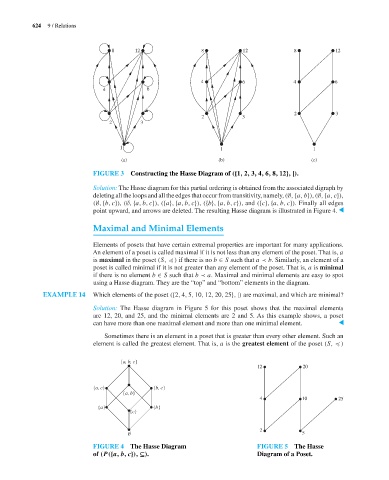
8 12 8 12 8 12

4 6 4 6
4 6

2 3
2 3
2 3

1 1 1
(a) (b) (c)

FIGURE 3 Constructing the Hasse Diagram of ({1, 2, 3, 4, 6, 8, 12}, |).

Solution: The Hasse diagram for this partial ordering is obtained from the associated digraph by
deleting all the loops and all the edges that occur from transitivity, namely, (∅, {a, b}), (∅, {a, c}),
(∅, {b, c}), (∅, {a, b, c}), ({a}, {a, b, c}), ({b}, {a, b, c}), and ({c}, {a, b, c}). Finally all edges
point upward, and arrows are deleted. The resulting Hasse diagram is illustrated in Figure 4. ▲

Maximal and Minimal Elements

Elements of posets that have certain extremal properties are important for many applications.
An element of a poset is called maximal if it is not less than any element of the poset. That is, a
is maximal in the poset (S, ) if there is no b ∈ S such that a ≺ b. Similarly, an element of a
poset is called minimal if it is not greater than any element of the poset. That is, a is minimal
if there is no element b ∈ S such that b ≺ a. Maximal and minimal elements are easy to spot
using a Hasse diagram. They are the “top” and “bottom” elements in the diagram.

EXAMPLE 14 Which elements of the poset ({2, 4, 5, 10, 12, 20, 25}, |) are maximal, and which are minimal?
Solution: The Hasse diagram in Figure 5 for this poset shows that the maximal elements
are 12, 20, and 25, and the minimal elements are 2 and 5. As this example shows, a poset
can have more than one maximal element and more than one minimal element. ▲

Sometimes there is an element in a poset that is greater than every other element. Such an
element is called the greatest element. That is, a is the greatest element of the poset (S, )

{a,b,c}
12 20

{a,c} {b, c}
{a,b}
4 10 25
{a} {b}
{c}

2
∅ 5

FIGURE 4 The Hasse Diagram FIGURE 5 The Hasse
of (P({a, b, c}), ⊆). Diagram of a Poset.