Page 298 -

HAN
2011/6/1
3:20 Page 261
#19
13-ch06-243-278-9780123814791
6.2 Frequent Itemset Mining Methods 261

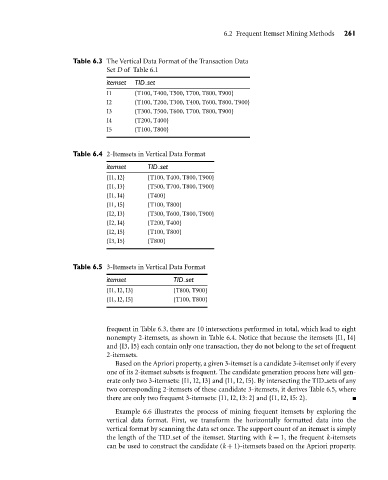
Table 6.3 The Vertical Data Format of the Transaction Data
Set D of Table 6.1
itemset TID set
I1 {T100, T400, T500, T700, T800, T900}
I2 {T100, T200, T300, T400, T600, T800, T900}
I3 {T300, T500, T600, T700, T800, T900}
I4 {T200, T400}
I5 {T100, T800}

Table 6.4 2-Itemsets in Vertical Data Format
itemset TID set
{I1, I2} {T100, T400, T800, T900}
{I1, I3} {T500, T700, T800, T900}
{I1, I4} {T400}
{I1, I5} {T100, T800}
{I2, I3} {T300, T600, T800, T900}
{I2, I4} {T200, T400}
{I2, I5} {T100, T800}
{I3, I5} {T800}

Table 6.5 3-Itemsets in Vertical Data Format
itemset TID set
{I1, I2, I3} {T800, T900}
{I1, I2, I5} {T100, T800}

frequent in Table 6.3, there are 10 intersections performed in total, which lead to eight
nonempty 2-itemsets, as shown in Table 6.4. Notice that because the itemsets {I1, I4}
and {I3, I5} each contain only one transaction, they do not belong to the set of frequent
2-itemsets.
Based on the Apriori property, a given 3-itemset is a candidate 3-itemset only if every
one of its 2-itemset subsets is frequent. The candidate generation process here will gen-
erate only two 3-itemsets: {I1, I2, I3} and {I1, I2, I5}. By intersecting the TID sets of any
two corresponding 2-itemsets of these candidate 3-itemsets, it derives Table 6.5, where
there are only two frequent 3-itemsets: {I1, I2, I3: 2} and {I1, I2, I5: 2}.

Example 6.6 illustrates the process of mining frequent itemsets by exploring the
vertical data format. First, we transform the horizontally formatted data into the
vertical format by scanning the data set once. The support count of an itemset is simply
the length of the TID set of the itemset. Starting with k = 1, the frequent k-itemsets
can be used to construct the candidate (k + 1)-itemsets based on the Apriori property.