Page 271 - Design for Six Sigma a Roadmap for Product Development

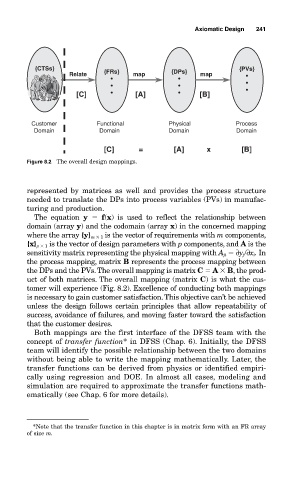
Axiomatic Design 241

{CTSs} {PVs}
DPs}
. . Relate {FRs} map {DPs} map •
. . • • •
. . • • •
[C] • [A] • [B]

Customer Functional Physical Process
Domain Domain Domain Domain

[C] = [A] x [B]

Figure 8.2 The overall design mappings.

represented by matrices as well and provides the process structure
needed to translate the DPs into process variables (PVs) in manufac-
turing and production.
The equation y f(x) is used to reflect the relationship between
domain (array y) and the codomain (array x) in the concerned mapping
where the array {y} m
1 is the vector of requirements with m components,
{x} p
1 is the vector of design parameters with p components, and A is the
sensitivity matrix representing the physical mapping with A ji ∂y j /∂x i . In
the process mapping, matrix B represents the process mapping between
the DPs and the PVs.The overall mapping is matrix C A
B, the prod-
uct of both matrices. The overall mapping (matrix C) is what the cus-
tomer will experience (Fig. 8.2). Excellence of conducting both mappings
is necessary to gain customer satisfaction.This objective can’t be achieved
unless the design follows certain principles that allow repeatability of
success, avoidance of failures, and moving faster toward the satisfaction
that the customer desires.
Both mappings are the first interface of the DFSS team with the
concept of transfer function* in DFSS (Chap. 6). Initially, the DFSS
team will identify the possible relationship between the two domains
without being able to write the mapping mathematically. Later, the
transfer functions can be derived from physics or identified empiri-
cally using regression and DOE. In almost all cases, modeling and
simulation are required to approximate the transfer functions math-
ematically (see Chap. 6 for more details).

*Note that the transfer function in this chapter is in matrix form with an FR array
of size m.