Page 584 - Design for Six Sigma a Roadmap for Product Development
P. 584
Design Optimization: Advanced Taguchi Robust Parameter Design 541
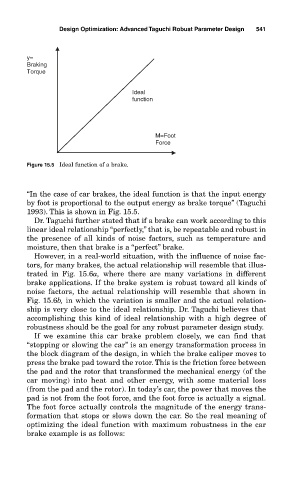
y=
Braking
Torque
Ideal
function
M=Foot
Force
Figure 15.5 Ideal function of a brake.
“In the case of car brakes, the ideal function is that the input energy
by foot is proportional to the output energy as brake torque” (Taguchi
1993). This is shown in Fig. 15.5.
Dr. Taguchi further stated that if a brake can work according to this
linear ideal relationship “perfectly,” that is, be repeatable and robust in
the presence of all kinds of noise factors, such as temperature and
moisture, then that brake is a “perfect” brake.
However, in a real-world situation, with the influence of noise fac-
tors, for many brakes, the actual relationship will resemble that illus-
trated in Fig. 15.6a, where there are many variations in different
brake applications. If the brake system is robust toward all kinds of
noise factors, the actual relationship will resemble that shown in
Fig. 15.6b, in which the variation is smaller and the actual relation-
ship is very close to the ideal relationship. Dr. Taguchi believes that
accomplishing this kind of ideal relationship with a high degree of
robustness should be the goal for any robust parameter design study.
If we examine this car brake problem closely, we can find that
“stopping or slowing the car” is an energy transformation process in
the block diagram of the design, in which the brake caliper moves to
press the brake pad toward the rotor. This is the friction force between
the pad and the rotor that transformed the mechanical energy (of the
car moving) into heat and other energy, with some material loss
(from the pad and the rotor). In today’s car, the power that moves the
pad is not from the foot force, and the foot force is actually a signal.
The foot force actually controls the magnitude of the energy trans-
formation that stops or slows down the car. So the real meaning of
optimizing the ideal function with maximum robustness in the car
brake example is as follows: