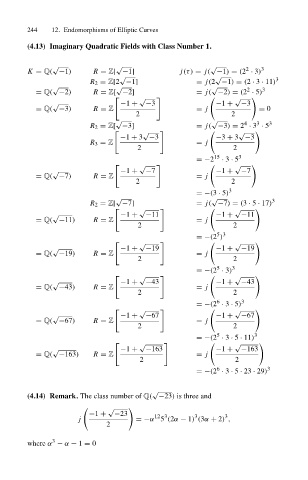Page 267 -

244 12. Endomorphisms of Elliptic Curves

(4.13) ImaginaryQuadratic Fields with Class Number 1.

√ √ √
2
K = Q( −1) R = Z[ −1] j(τ) = j( −1) = (2 · 3) 3
√ √
R 2 = Z[2 −1] = j(2 −1) = (2 · 3 · 11) 3
√ √ √ 2 3
= Q( −2) R = Z[ −2] = j( −2) = (2 · 5)
√ √
√ −1 + −3 −1 + −3
= Q( −3) R = Z = j = 0
2 2
√ √
3
4
R 2 = Z[ −3] = j( −3) = 2 · 3 · 5 3
√ √

−1 + 3 −3 −3 + 3 −3
R 3 = Z = j
2 2
=−2 15 · 3 · 5 3
√ √

√ −1 + −7 −1 + −7
= Q( −7) R = Z = j
2 2
=−(3 · 5) 3
√ √
R 2 = Z[ −7] = j( −7) = (3 · 5 · 17) 3
√ √
√ −1 + −11 −1 + −11
= Q( −11) R = Z = j
2 2
5 3
=−(2 )
√ √

√ −1 + −19 −1 + −19
= Q( −19) R = Z = j
2 2
5
=−(2 · 3) 3
√ √

√ −1 + −43 −1 + −43
= Q( −43) R = Z = j
2 2
6
=−(2 · 3 · 5) 3
√ √
√ −1 + −67 −1 + −67
= Q( −67) R = Z = j
2 2
5
=−(2 · 3 · 5 · 11) 3
√ √
√ −1 + −163 −1 + −163
= Q( −163) R = Z = j
2 2
6
=−(2 · 3 · 5 · 23 · 29) 3
√
(4.14) Remark. The class number of Q( −23) is three and
√

−1 + −23 12 3 3 3
j =−α 5 (2α − 1) (3α + 2) ,
2
3
where α − α − 1 = 0