Page 24 - Engineering Electromagnetics, 8th Edition

6 ENGINEERING ELECTROMAGNETICS

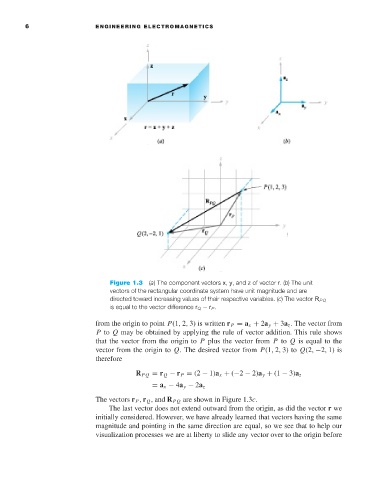
Figure 1.3 (a) The component vectors x, y, and z of vector r.(b) The unit
vectors of the rectangular coordinate system have unit magnitude and are
directed toward increasing values of their respective variables. (c) The vector R PQ
is equal to the vector difference r Q − r P .

from the origin to point P(1, 2, 3) is written r P = a x + 2a y + 3a z . The vector from
P to Q may be obtained by applying the rule of vector addition. This rule shows
that the vector from the origin to P plus the vector from P to Q is equal to the
vector from the origin to Q. The desired vector from P(1, 2, 3) to Q(2, −2, 1) is
therefore

R PQ = r Q − r P = (2 − 1)a x + (−2 − 2)a y + (1 − 3)a z
= a x − 4a y − 2a z
The vectors r P , r Q , and R PQ are shown in Figure 1.3c.
The last vector does not extend outward from the origin, as did the vector r we
initially considered. However, we have already learned that vectors having the same
magnitude and pointing in the same direction are equal, so we see that to help our
visualization processes we are at liberty to slide any vector over to the origin before