Page 80 - Essentials of applied mathematics for scientists and engineers

book Mobk070 March 22, 2007 11:7

70 ESSENTIALS OF APPLIED MATHEMATICS FOR SCIENTISTS AND ENGINEERS
n = 1 c n = 0 when n ≥ 1 and the polynomial is x. In general

n(n − 1) n(n − 1)(n − 2)(n − 3)

n n−2 n−4
u = P n (x) = c n x − x + x − ...
2(2n − 1) 2(4)(2n − 1)(2n − 3)
m k
1 (−1) (2n − 2k)! n−2k
= x (4.138)
2 k k! (n − 2k)!(n − k)!
k=0
where m = n/2if n is even and (n − 1)/2if n is odd.
The coefficient c n is of course arbitrary. It turns out to be convenient to choose it to be

c 0 = 1
(2n − 1)(2n − 3) ··· 1
c n = (4.139)
n!
the first few polynomials are
3
4
2
2
P 0 = 1, P 1 = x, P 2 = (3x − 1)/2, P 3 = (5x − 3x)/2, P 4 = (35x − 30x + 3)/8,
Successive Legendre polynomials can be generated by the use of Rodrigues’ formula
1 d n 2 n
P n (x) = (x − 1) (4.140)
n
2 n! dx n
For example

3
5
P 5 = (63x − 70x + 15x)/8
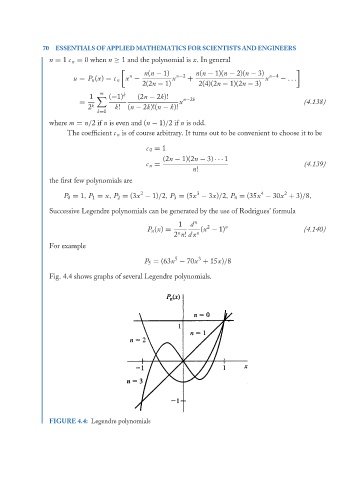
Fig. 4.4 shows graphs of several Legendre polynomials.

FIGURE 4.4: Legendre polynomials