Page 268 - Essentials of physical chemistry

230 Essentials of Physical Chemistry

30 15 0 15 30

Co-latitude angle
45
68
45
Primary beam 40

60 60
65 64 60
60
54
62
70
68
75
68 48
75
44
40
90
90
{1, 0, 0} azimuth Target {1, 1, 1} azimuth
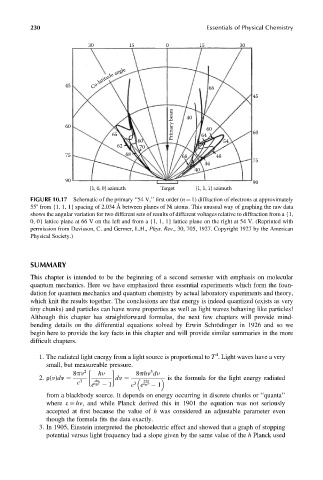
FIGURE 10.17 Schematic of the primary ‘‘54 V,’’ first order (n ¼ 1) diffraction of electrons at approximately
558 from {1, 1, 1} spacing of 2.034 Å between planes of Ni atoms. This unusual way of graphing the raw data
shows the angular variation for two different sets of results of different voltages relative to diffraction from a {1,
0, 0} lattice plane at 66 V on the left and from a {1, 1, 1} lattice plane on the right at 54 V. (Reprinted with
permission from Davisson, C. and Germer, L.H., Phys. Rev., 30, 705, 1927. Copyright 1927 by the American
Physical Society.)

SUMMARY

This chapter is intended to be the beginning of a second semester with emphasis on molecular
quantum mechanics. Here we have emphasized three essential experiments which form the foun-
dation for quantum mechanics and quantum chemistry by actual laboratory experiments and theory,
which knit the results together. The conclusions are that energy is indeed quantized (exists as very
tiny chunks) and particles can have wave properties as well as light waves behaving like particles!
Although this chapter has straightforward formulas, the next few chapters will provide mind-
bending details on the differential equations solved by Erwin Schrödinger in 1926 and so we
begin here to provide the key facts in this chapter and will provide similar summaries in the more
difficult chapters.
4
1. The radiated light energy from a light source is proportional to T . Light waves have a very
small, but measureable pressure.
3
8pn 2 hn 8phn dn
is the formula for the light energy radiated
c e B T 1 c e B T 1
2. r(n)dn ¼ 3 hn dn ¼ þhn
3
k
k
from a blackbody source. It depends on energy occurring in discrete chunks or ‘‘quanta’’
where e ¼ hn, and while Planck derived this in 1901 the equation was not seriously
accepted at first because the value of h was considered an adjustable parameter even
though the formula fits the data exactly.
3. In 1905, Einstein interpreted the photoelectric effect and showed that a graph of stopping
potential versus light frequency had a slope given by the same value of the h Planck used