Page 28 - Fluid Mechanics and Thermodynamics of Turbomachinery

Introduction: Dimensional Analysis: Similitude 9
The non-dimensional results shown in Figure 1.3 have, of course, been obtained
for a particular pump. They would also be approximately valid for a range of
different pump sizes so long as all these pumps are geometrically similar and cavi-
tation is absent. Thus, neglecting any change in performance due to change in
Reynolds number, the dynamically similar results in Figure 1.3 can be applied to
predicting the dimensional performance of a given pump for a series of required
speeds. Figure 1.4 shows such a dimensional presentation. It will be clear from the
above discussion that the locus of dynamically similar points in the H Q field lies
2
on a parabola since H varies as N and Q varies as N.

Variable geometry turbomachines

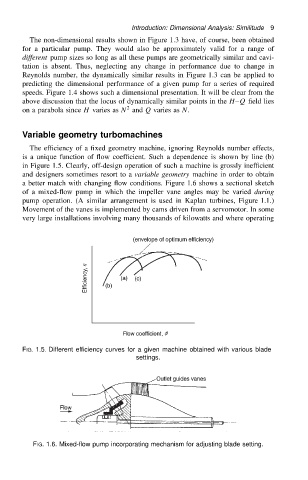
The efficiency of a fixed geometry machine, ignoring Reynolds number effects,
is a unique function of flow coefficient. Such a dependence is shown by line (b)
in Figure 1.5. Clearly, off-design operation of such a machine is grossly inefficient
and designers sometimes resort to a variable geometry machine in order to obtain
a better match with changing flow conditions. Figure 1.6 shows a sectional sketch
of a mixed-flow pump in which the impeller vane angles may be varied during
pump operation. (A similar arrangement is used in Kaplan turbines, Figure 1.1.)
Movement of the vanes is implemented by cams driven from a servomotor. In some
very large installations involving many thousands of kilowatts and where operating

FIG. 1.5. Different efficiency curves for a given machine obtained with various blade
settings.

FIG. 1.6. Mixed-flow pump incorporating mechanism for adjusting blade setting.