Page 115 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 115
PIPES CONVEYING FLUID: LINEAR DYNAMICS I 97
\ 15 f U2IT2
\
-10.
\
\
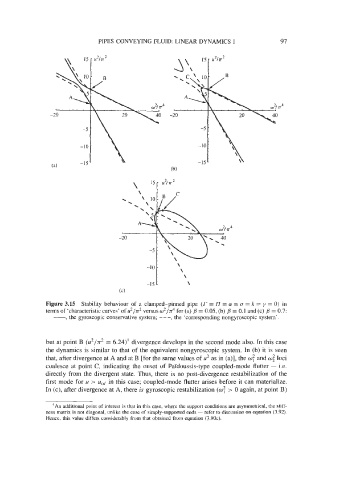
Figure 3.15 Stability behaviour of a clamped-pinned pipe (r = 17 = a = n = k = y = 0) in
terms of ‘characteristic curves’ of u2/n2 versus w2/n4 for (a) p = 0.05, (b) p = 0.1 and (c) p = 0.7:
-, the gyroscopic conservative system; - - -, the ‘corresponding nongyroscopic system’.
but at point B (u2/n2 = 6.24)’ divergence develops in the second mode also. In this case
the dynamics is similar to that of the equivalent nongyroscopic system. In (b) it is seen
that, after divergence at A and at B [for the same values of u2 as in (a)], the w: and wi loci
coalesce at point C, indicating the onset of Paldoussis-type coupled-mode flutter - i.e.
directly from the divergent state. Thus, there is no post-divergence restabilization of the
first mode for u > u,d in this case; coupled-mode flutter arises before it can materialize.
In (c), after divergence at A, there is gyroscopic restabilization (w: > 0 again, at point B)
‘An additional point of interest is that in this case, where the support conditions are asymmetrical, the stiff-
ness matrix is not diagonal, unlike the case of simply-supported ends - refer to discussion on equation (3.92).
Hence, this value differs considerably from that obtained from equation (3.90~).