Page 36 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 36
CONCEPTS. DEFINITIONS AND METHODS 19
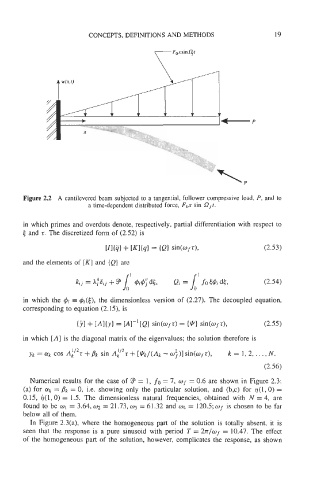
Figure 2.2 A cantilevered beam subjected to a tangential, follower compressive load, P, and to
a time-dependent distributed force, Fox sin aft.
in which primes and overdots denote, respectively, partial differentiation with respect to
6 and r. The discretized form of (2.52) is
and the elements of [K] and {Q] are
(2.54)
in which the $i E $;(e), the dimensionless version of (2.27). The decoupled equation,
corresponding to equation (2.15), is
(y] + [Al{y} = [A]-’(Q] sin(wft) = (!PI sin(wfr), (2.55)
in which [A] is the diagonal matrix of the eigenvalues; the solution therefore is
yk = (Ilk COS A:”t + pk Sin AL’2t + [!Pk/(Ak - W;)] Sin(wf t), k = 1, 2, . . . , N.
(2.56)
Numerical results for the case of 8 = 1, fo = 7, Wf = 0.6 are shown in Figure 2.3:
(a) for (Ilk = pk = 0, i.e. showing only the particular solution, and (b,c) for q(1,O) =
0.15, li(l, 0) = 1.5. The dimensionless natural frequencies, obtained with N = 4, are
found to be w1 = 3.64, w;! = 21.73,03 = 61.32 and 04 = 120.5;wf is chosen to be far
below all of them.
In Figure 2.3(a), where the homogeneous part of the solution is totally absent, it is
seen that the response is a pure sinusoid with period T = 21r/of = 10.47. The effect
of the homogeneous part of the solution, however, complicates the response, as shown