Page 70 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

CONCEPTS, DEFINJTIONS AND METHODS 53
the branch associated with negative frequency, being more mathematical than physical, is
often suppressed; nevertheless, the bifurcation of the eigenfrequency locus in the upper-right
panel of Figure 2.10 is more easily comprehensible if both branches are shown.
Linear theory can only predict the onset of divergence or flutter; solution (2.163) with
%ne@) > 0 or 4m(Q) < 0 would suggest that the motion is amplified indefinitely. This
is normally not so, but it is only through nonlinear theory that we can discover what
happens. We know physically that a column subjected to a compressive load or a pipe with
supported ends conveying fluid will diverge to one side or the other and then display a new,
buckled equilibrium form. In nonlinear theory the linear instability is simply referred to as
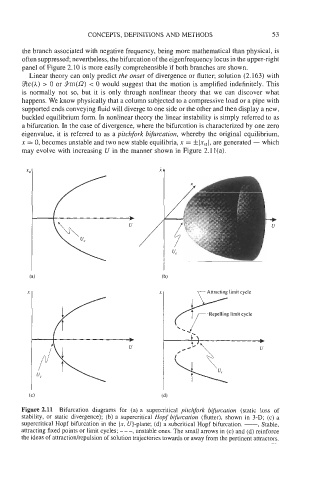
a bifurcation. In the case of divergence, where the bifurcation is characterized by one zero
eigenvalue, it is referred to as a pitchfork bifurcation, whereby the original equilibrium,
x = 0, becomes unstable and two new stable equilibria, x = f IxSt I, are generated - which
may evolve with increasing U in the manner shown in Figure 2.1 l(a>.

--&
U

X Attracting limit cycle

Figure 2.11 Bifurcation diagrams for (a) a supercritical pitchfork bifurcafion (static loss of
stability, or static divergence); (b) a supercritical Hopf bificrcation (flutter), shown in 3-D; (c) a
supercritical Hopf bifurcation in the (x, (I)-plane; (d) a subcritical Hopf bifurcation. -, Stable,
attracting fixed points or limit cycles; ---, unstable ones. The small arrows in (c) and (d) reinforce
the ideas of attractiodrepulsion of solution trajectories towards or away from the pertinent attractors.