Page 85 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

68 SLENDER STRUCTURES AND AXIAL FLOW

d ruc

r'

(C) (4
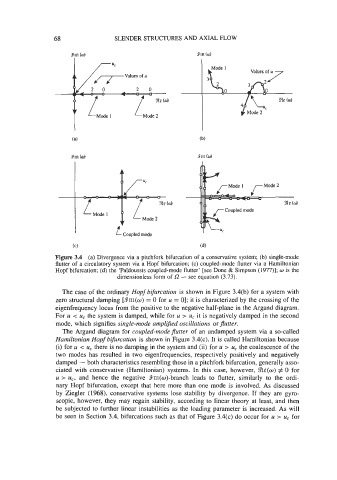
Figure 3.4 (a) Divergence via a pitchfork bifurcation of a conservative system; (b) single-mode
flutter of a circulatory system via a Hopf bifurcation; (c) coupled-mode flutter via a Hamiltonian
Hopf bifurcation; (d) the 'Pai'doussis coupled-mode flutter' [see Done & Simpson (1977)l; w is the
dimensionless form of 52 - see equation (3.73).
The case of the ordinary Hopfbifurcation is shown in Figure 3.4(b) for a system with
zero structural damping [Sint(o) = 0 for u = 01; it is characterized by the crossing of the
eigenfrequency locus from the positive to the negative half-plane in the Argand diagram.
For u < u, the system is damped, while for u u, it is negatively damped in the second
mode, which signifies single-mode amplijied oscillations or flutrer.
The Argand diagram for coupled-modeflutter of an undamped system via a so-called
Hamiltonian Hopf bifurcation is shown in Figure 3.4(c). It is called Hamiltonian because
(i) for u < u, there is no damping in the system and (ii) for u > u, the coalescence of the
two modes has resulted in two eigenfrequencies, respectively positively and negatively
damped - both characteristics resembling those in a pitchfork bifurcation, generally asso-
ciated with conservative (Hamiltonian) systems. In this case, however, %e(o) # 0 for
u > u,, and hence the negative Snt(w)-branch leads to flutter, similarly to the ordi-
nary Hopf bifurcation, except that here more than one mode is involved. As discussed
by Ziegler (1968). conservative systems lose stability by divergence. If they are gyro-
scopic, however, they may regain stability, according to linear theory at least, and then
be subjected to further linear instabilities as the loading parameter is increased. As will
be seen in Section 3.4, bifurcations such as that of Figure 3.4(c) do occur for u > u, for