Page 393 - Fundamentals of Magnetic Thermonuclear Reactor Design

Mechanics of Magnetic Fusion Reactors Chapter | 12 371

The intensity of external effects on the VV components varies as the dis-
charge proceeds, which makes dynamic computations an important part of
the design process. This includes the development and verification of special
computational software with a mandatory validation of obtained results. For
instance, ITER design experience has proved that a finite-element model of a
40-degree VV segment is quite sufficient to obtain an adequate mechanical re-
sponse of the VV to a cyclically symmetric electromagnetic loading. In the case
of an asymmetric loading, a 180-degree model is required.
The most accurate VV dynamic response to pulsed EMLs is obtained with
the direct step-by-step integration method. When using the modal superposition
technique, one should account for too many types of free oscillations, which
takes its toll on the calculation accuracy.
As a rule, the VV constructional elements are subjected to electromagnetic
and thermomechanical cyclic loads simultaneously. Short-term (from a few
milliseconds to 10 s) EMLs may overlap longer (from a few tens to a few hun-
dreds of seconds) thermal stresses. This complicates the VV structural analysis
and life-time assessment.
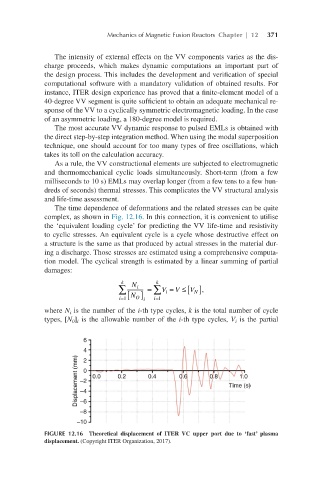
The time dependence of deformations and the related stresses can be quite
complex, as shown in Fig. 12.16. In this connection, it is convenient to utilise
the ‘equivalent loading cycle’ for predicting the VV life-time and resistivity
to cyclic stresses. An equivalent cycle is a cycle whose destructive effect on
a structure is the same as that produced by actual stresses in the material dur-
ing a discharge. Those stresses are estimated using a comprehensive computa-
tion model. The cyclical strength is estimated by a linear summing of partial
damages:
k N k
∑ i = ∑ i = V ≤ V N
[ ],
V
= i 1 [N O ] i = i 1 ∑i=1kNiN i=∑i=1kVi=V≤VN,
0
where N is the number of the i-th type cycles, k is the total number of cycle
i
types, [N ] is the allowable number of the i-th type cycles, V is the partial
i
0 i

FIGURE 12.16 Theoretical displacement of ITER VC upper port due to ‘fast’ plasma
displacement. (Copyright ITER Organization, 2017).