Page 250 - Fundamentals of Ocean Renewable Energy Generating Electricity From The Sea

240 Fundamentals of Ocean Renewable Energy

For instance, assume that the location of four wind turbines in an offshore
wind farm needs to be optimized. For this problem, the objective function can
be defined as electricity production. The decision variables are the geographical
coordinates of these four turbines: (x 1 , y 1 ; x 2 , y 2 ; x 3 , y 3 ; x 4 , y 4 ). The production
of electricity in this small array depends on the decision variables, because both
the available wind energy resource, and the wake of each turbine (that may
adversely affect power output for another turbine) are controlled by turbine
locations. The feasible space or constraints can be defined as the leased area
of the farm, because none of these turbines can be installed outside the allocated
area. This can be mathematically formulated as a ≤ x i ≤ b and c ≤ y i ≤ d,
where a, b, c, and d define the geographical boundaries of this problem. This
type of constraint is called inequality constraint. Equality constraints can also be
applied. For the simple wind farm example, assume that, for aesthetic reasons,
we want to install all four turbines in a straight line. Therefore, the geographical
locations of all turbines must satisfy the equation of a line (i.e. mx i +ny i +q = 0).
In general, an optimization problem can be formulated as
minimize f(x 1 , x 2 , ... , x n ) (9.2)
subject to g k (x 1 , x 2 , ... , x n ) ≥ 0 k = 1, 2, ... , N c 1 ;
h l (x 1 , x 2 , ... , x n ) = 0 l = 1, 2, ... , N c 2
where g k and h k represent inequality and equality constraints of the problem.
are the number of inequality and quality constraints, respectively;
N c 1 and N c 2
an optimization problem can have several inequality or equality constraints. It
should be noted that applying too many constraints can make an optimization
problem infeasible (e.g. if constraints are mutually contradictory), and so result
in no solution.
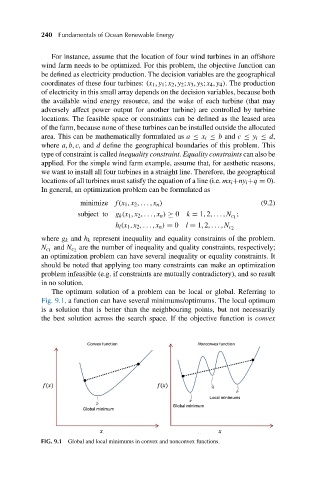
The optimum solution of a problem can be local or global. Referring to
Fig. 9.1, a function can have several minimums/optimums. The local optimum
is a solution that is better than the neighbouring points, but not necessarily
the best solution across the search space. If the objective function is convex

FIG. 9.1 Global and local minimums in convex and nonconvex functions.