Page 156 - Fundamentals of Physical Volcanology

9780632054435_4_009.qxd 12/10/2007 12:31PM Page 133

LAVA FLOWS 133

that makes predicting the behavior of lava flows
very difficult.
D
B
9.5 Rheological control of lava flow geometry
Shear stress F1 F2 It has generally been assumed that there is no need

to consider rheological properties any more
complex than those of Bingham fluid to describe
N
lava flows. Indeed, early work on the properties of
flows recognized that if it was assumed that lava
T was a Bingham plastic material, there was a natural
reason for the observation that flows spread side-
ways to reach a well-defined width and then form
Strain rate
levées that do not change their shape. This is illus-
trated in Fig. 9.13, which shows the components
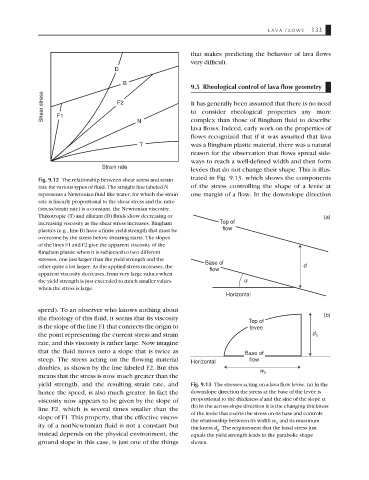
Fig. 9.12 The relationship between shear stress and strain
rate for various types of fluid. The straight line labeled N of the stress controlling the shape of a levée at
represents a Newtonian fluid like water, for which the strain one margin of a flow. In the downslope direction
rate is linearly proportional to the shear stress and the ratio
(stress/strain rate) is a constant, the Newtonian viscosity.
Thixotropic (T) and dilatant (D) fluids show decreasing or (a)
increasing viscosity as the shear stress increases. Bingham Top of
plastics (e.g., line B) have a finite yield strength that must be flow
overcome by the stress before shearing starts. The slopes
of the lines F1 and F2 give the apparent viscosity of the
Bingham plastic when it is subjected to two different
stresses, one just larger than the yield strength and the
Base of
other quite a lot larger. As the applied stress increases, the d
flow
apparent viscosity decreases, from very large values when
the yield strength is just exceeded to much smaller values a
when the stress is large.
Horizontal
speed). To an observer who knows nothing about
(b)
the rheology of this fluid, it seems that its viscosity
Top of
is the slope of the line F1 that connects the origin to levee
the point representing the current stress and strain d b
rate, and this viscosity is rather large. Now imagine
that the fluid moves onto a slope that is twice as Base of
steep. The stress acting on the flowing material flow
Horizontal
doubles, as shown by the line labeled F2. But this
w b
means that the stress is now much greater than the
yield strength, and the resulting strain rate, and Fig. 9.13 The stresses acting on a lava flow levée. (a) In the
hence the speed, is also much greater. In fact the downslope direction the stress at the base of the levée is
viscosity now appears to be given by the slope of proportional to the thickness d and the sine of the slope α.
(b) In the across-slope direction it is the changing thickness
line F2, which is several times smaller than the
of the levée that exerts the stress on its base and controls
slope of F1. This property, that the effective viscos-
the relationship between its width w and its maximum
b
ity of a nonNewtonian fluid is not a constant but
thickness d . The requirement that the basal stress just
b
instead depends on the physical environment, the equals the yield strength leads to the parabolic shape
ground slope in this case, is just one of the things shown.