Page 83 - Fundamentals of Physical Volcanology

9780632054435_4_004.qxd 12/10/2007 12:19PM Page 60

60 CHAPTER 4

Figures 4.7 and 4.8 illustrated geophysical stud- within the volcanic system and increases the cham-
ies of volcanoes showing that magma chambers ber pressure. The amount of magma that can be
inflate prior to eruption as fresh magma is added added to a chamber of given size before failure
to them. When some critical point is reached occurs is given by
the chamber ruptures and a dike is emplaced. As
the dike propagates, magma is withdrawn from the ∆V/V = [(σ /β) (1 + s)] + s (4.3)
c T
chamber causing deflation. If the dike reaches the
surface then an eruption will result. Various mathe- where ∆V is the volume of magma added to the
matical models have been developed to look at chamber, V is the initial chamber volume, β is the
c
the nature and consequences of the failure or rup- bulk modulus of the magma (the reciprocal of its
ture of magma chambers. The general features of compressibility) and s is the fractional increase in
such models can be illustrated by the following chamber volume which can be achieved inelast-
one, due to Stephen Blake. The criterion for failure ically, that is, without compressing the rocks sur-
of the walls of a magma chamber (approximated as rounding the chamber (perhaps by the closure of any
a sphere) is that the stress difference across the open pore spaces present in the surrounding rocks).
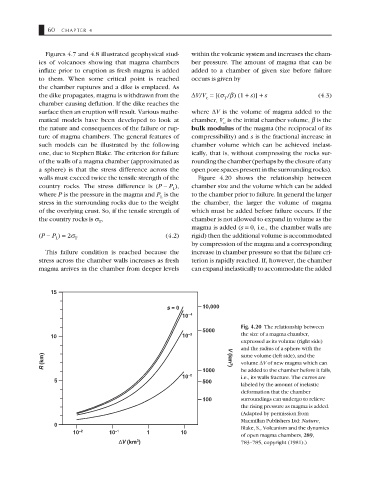
walls must exceed twice the tensile strength of the Figure 4.20 shows the relationship between
country rocks. The stress difference is (P − P ), chamber size and the volume which can be added
L
where P is the pressure in the magma and P is the to the chamber prior to failure. In general the larger
L
stress in the surrounding rocks due to the weight the chamber, the larger the volume of magma
of the overlying crust. So, if the tensile strength of which must be added before failure occurs. If the
the country rocks is σ , chamber is not allowed to expand in volume as the
T
magma is added (s = 0, i.e., the chamber walls are
(P − P ) = 2σ (4.2) rigid) then the additional volume is accommodated
L T
by compression of the magma and a corresponding
This failure condition is reached because the increase in chamber pressure so that the failure cri-
stress across the chamber walls increases as fresh terion is rapidly reached. If, however, the chamber
magma arrives in the chamber from deeper levels can expand inelastically to accommodate the added

15

s = 0 10,000
10 –4
Fig. 4.20 The relationship between
5000
10 10 –3 the size of a magma chamber,
expressed as its volume (right side)
and the radius of a sphere with the
R (km) V (km 3 ) same volume (left side), and the
volume ∆V of new magma which can

10 –2 1000 be added to the chamber before it fails,
i.e., its walls fracture. The curves are
5 500
labeled by the amount of inelastic
deformation that the chamber
100 surroundings can undergo to relieve
the rising pressure as magma is added.
(Adapted by permission from
Macmillan Publishers Ltd: Nature,
0
Blake, S., Volcanism and the dynamics
10 –2 10 –1 1 10
of open magma chambers, 289,
3
D V (km ) 783–785, copyright (1981).)