Page 341 - Hardware Implementation of Finite-Field Arithmetic

Optimal Extension Fields 321

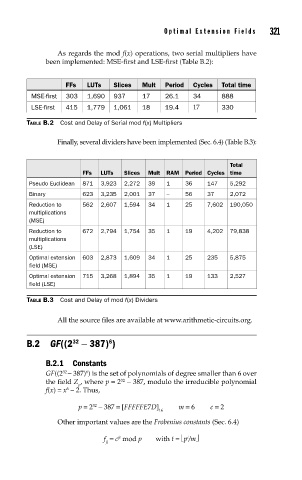
As regards the mod f(x) operations, two serial multipliers have
been implemented: MSE-first and LSE-first (Table B.2):

FFs LUTs Slices Mult Period Cycles Total time
MSE-first 303 1,690 937 17 26.1 34 888
LSE-first 415 1,779 1,061 18 19.4 17 330

TABLE B.2 Cost and Delay of Serial mod f(x) Multipliers

Finally, several dividers have been implemented (Sec. 6.4) (Table B.3):

Total
FFs LUTs Slices Mult RAM Period Cycles time
Pseudo Euclidean 871 3,923 2,272 39 1 36 147 5,292
Binary 623 3,235 2,001 37 − 56 37 2,072
Reduction to 562 2,607 1,594 34 1 25 7,602 190,050
multiplications
(MSE)
Reduction to 672 2,794 1,754 35 1 19 4,202 79,838
multiplications
(LSE)
Optimal extension 603 2,873 1,609 34 1 25 235 5,875
field (MSE)
Optimal extension 715 3,268 1,894 35 1 19 133 2,527
field (LSE)

TABLE B.3 Cost and Delay of mod f(x) Dividers

All the source files are available at www.arithmetic-circuits.org.

6
32
B.2 GF((2 − 387) )
B.2.1 Constants
6
32
GF((2 − 387) ) is the set of polynomials of degree smaller than 6 over
32
the field Z , where p = 2 − 387, modulo the irreducible polynomial
p
f(x) = x − 2. Thus,
6
p = 2 − 387 = [FFFFFE7D] m = 6 c = 2
32
16
Other important values are the Frobenius constants (Sec. 6.4)
f = c mod p with t = ⎣p /m⎦
i
jt
ji