Page 463 - High Power Laser Handbook

430 Fi b er L a s er s Intr oduction to Optical Fiber Lasers 431

1.0 1.0
4.5 P /P CR = 0.1
0
0.8 0.8
0.5
2.5
0.6 2 0.6
ω/ω 0 V = 1.5 ω/ω 0
0.4 0.4
0.2 0.2
5 2 1
0.0 0.0
0.0 0.2 0.4 0.6 0.8 1.0 0 1 2 3 4
P /P CR z/z R
0
(a) (b)
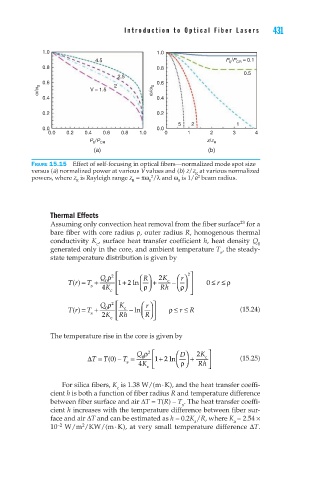
Figure 15.15 Effect of self-focusing in optical fibers—normalized mode spot size
versus (a) normalized power at various V values and (b) z/z at various normalized
R
2
powers, where z is Rayleigh range z = πω /λ and ω is 1/e beam radius.
2
R R 0 0

Thermal Effects
Assuming only convection heat removal from the fiber surface for a
23
bare fiber with core radius ρ, outer radius R, homogenous thermal
conductivity K , surface heat transfer coefficient h, heat density Q
0
c
generated only in the core, and ambient temperature T , the steady-
s
state temperature distribution is given by
Q ρ 2   R 2 K r   2 2 
+
Tr () = T + 0  12 ln + c −  0 ≤≤r ρ
  ρ
ρ
 
s 4 K c     Rh    
Q ρ  K   r 
2
= Tr () s + T 0  c − ln   ρ ≤≤ R (15.24)
r
2K c  Rh  R  
The temperature rise in the core is given by
Q ρ 2    2 K 
D
+ ln
∆= T()0 − s = T 4 0  12   + c  (15.25)
T
ρ
K c    Rh 
For silica fibers, K is 1.38 W/(m · K), and the heat transfer coeffi-
c
cient h is both a function of fiber radius R and temperature difference
between fiber surface and air ∆T = T(R) – T . The heat transfer coeffi-
s
cient h increases with the temperature difference between fiber sur-
face and air ∆T and can be estimated as h = 0.2K /R, where K = 2.54 ×
a
a
2
10 W/m /KW/(m · K), at very small temperature difference ∆T.
–2