Page 255 - Hydrocarbon

242 Tubing Performance

the vertical pressure drop in the tubing due to the hydrostatic pressure of the fluid
in the tubing and friction pressure drops, a certain flowing wellbore pressure is
required. For a single phase fluid (e.g. just water or just gas), this combination of
hydrostatic and friction is relatively straightforward to calculate even accounting for
the variation of gas density with pressure. For most production wells however, the
complication is that there is more than one phase present and each phase has a
different density and viscosity. This is multiphase flow. At high velocities the phases
are chaotically mixed and essentially travel at the same velocity. The density and
viscosities are then averages, and the friction and hydrostatic pressures can
be calculated. Under these circumstances, the hydrostatic pressure does not change
with rate, but the frictional pressure drop will be dependent on velocity or rate
squared. At lower velocities, the phases tend to travel at different velocities. This
effect is called slippage. As the lighter fluids (such as gas) travel faster than the denser
phases such as water, the gas will spend less time in the tubing compared to the
liquids. The gas will therefore occupy less space and have correspondingly less effect
on the overall density. As the rate reduces, the overall density will therefore increase.
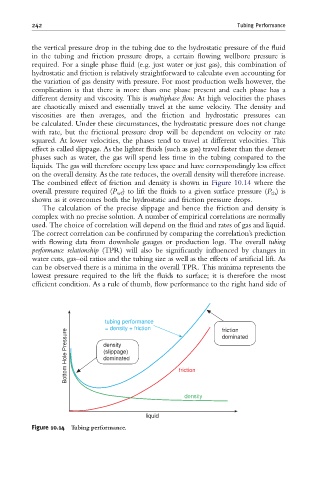
The combined effect of friction and density is shown in Figure 10.14 where the
overall pressure required (P wf ) to lift the fluids to a given surface pressure (P th )is
shown as it overcomes both the hydrostatic and friction pressure drops.
The calculation of the precise slippage and hence the friction and density is
complex with no precise solution. A number of empirical correlations are normally
used. The choice of correlation will depend on the fluid and rates of gas and liquid.
The correct correlation can be confirmed by comparing the correlation’s prediction
with flowing data from downhole gauges or production logs. The overall tubing
performance relationship (TPR) will also be significantly influenced by changes in
water cuts, gas–oil ratios and the tubing size as well as the effects of artificial lift. As
can be observed there is a minima in the overall TPR. This minima represents the
lowest pressure required to the lift the fluids to surface; it is therefore the most
efficient condition. As a rule of thumb, flow performance to the right hand side of

tubing performance
= density + friction friction
Bottom Hole Pressure density friction
dominated
(slippage)
dominated

density

liquid
Figure 10.14 Tubing performance.