Page 139 - Introduction to Continuum Mechanics

124 Polar Decomposition Theorem

becomes

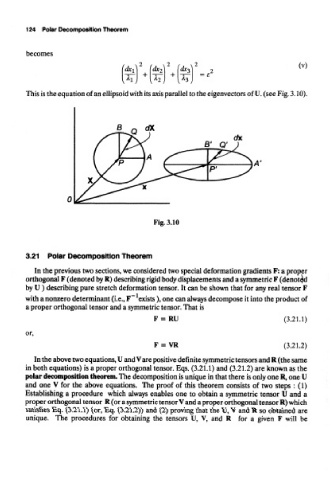
This is the equation of an ellipsoid with its axis parallel to the eigenvectors of U. (see Fig, 3.10).

Fig. 3.10

3.21 Polar Decomposition Theorem

In the previous two sections, we considered two special deformation gradients F: a proper
orthogonal F (denoted by R) describing rigid body displacements and a symmetric F (denoted
by U) describing pure stretch deformation tensor. It can be shown that for any real tensor F
with a nonzero determinant (i.e., F~ exists), one can always decompose it into the product of
a proper orthogonal tensor and a symmetric tensor. That is

or,

In the above two equations, U and V are positive definite symmetric tensors and R (the same
in both equations) is a proper orthogonal tensor. Eqs. (3.21.1) and (3.21.2) are known as the
polar decomposition theorem. The decomposition is unique in that there is only one R, one U
and one V for the above equations. The proof of this theorem consists of two steps : (1)
Establishing a procedure which always enables one to obtain a symmetric tensor U and a
proper orthogonal tensor R (or a symmetric tensor V and a proper orthogonal tensor R) which
satisfies Eq. (3.21.1) (or, Eq. (3.21.2)) and (2) proving that the U, V and R so obtained are
unique. TTie procedures for obtaining the tensors U, V, and R for a given F will be