Page 70 - Lindens Handbook of Batteries
P. 70
ELECTROCHEMICAL PRINCIPLES AND REACTIONS 2.27
100
1
ω max =
C dl R ct C dl
–Z i /Ω
R s
ω → ∞ ω → 0
0
0 Z r /Ω 100
R ct R s R s + R ct
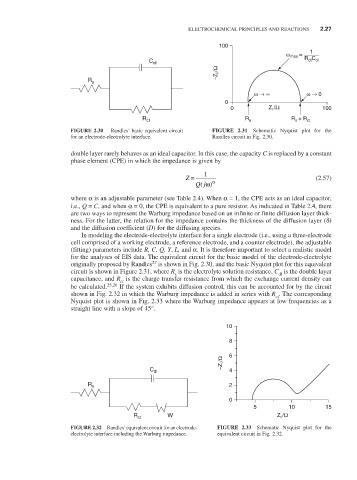
FIGURE 2.30 Randles’ basic equivalent circuit FIGURE 2.31 Schematic Nyquist plot for the
for an electrode-electrolyte interface. Randles circuit in Fig. 2.30.
double layer rarely behaves as an ideal capacitor. In this case, the capacity C is replaced by a constant
phase element (CPE) in which the impedance is given by
Z = 1 (2.57)
ω
(
Qj ) α
where α is an adjustable parameter (see Table 2.4). When α = 1, the CPE acts as an ideal capacitor,
i.e., Q = C, and when α = 0, the CPE is equivalent to a pure resistor. As indicated in Table 2.4, there
are two ways to represent the Warburg impedance based on an infinite or finite diffusion layer thick-
ness. For the latter, the relation for the impedance contains the thickness of the diffusion layer (δ)
and the diffusion coefficient (D) for the diffusing species.
In modeling the electrode-electrolyte interface for a single electrode (i.e., using a three-electrode
cell comprised of a working electrode, a reference electrode, and a counter electrode), the adjustable
(fitting) parameters include R, C, Q, Y, L, and α. It is therefore important to select a realistic model
for the analyses of EIS data. The equivalent circuit for the basic model of the electrode-electrolyte
27
originally proposed by Randles is shown in Fig. 2.30, and the basic Nyquist plot for this equivalent
circuit is shown in Figure 2.31, where R is the electrolyte solution resistance, C is the double layer
s
dl
capacitance, and R is the charge transfer resistance from which the exchange current density can
ct
be calculated. 25,26 If the system exhibits diffusion control, this can be accounted for by the circuit
shown in Fig. 2.32 in which the Warburg impedance is added in series with R . The corresponding
ct
Nyquist plot is shown in Fig. 2.33 where the Warburg impedance appears at low frequencies as a
straight line with a slope of 45°.
10
8
6
–Z i /Ω
C dl 4
2
R s
0
5 10 15
R ct W Z r /Ω
FIGURE 2.32 Randles’ equivalent circuit for an electrode- FIGURE 2.33 Schematic Nyquist plot for the
electrolyte interface including the Warburg impedance. equivalent circuit in Fig. 2.32.